Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.
Where the techniques of Maths
are explained in simple terms.
Trigonometry - Further trigonometric identities - angle sum and difference.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The results required for these further identities are:
sin (A ± B) = sin A cos B ± cos A sin B
cos (A + B) = cos A cos B - sinA sin B
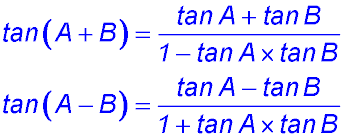
| Expanding terms. | Expand sin (2x + y). | Expand cos (2x - y). |
| Expand tan (4α - 3β). | Expand and simplify tan (A + 45°). |
|
| Find the exact value of sin (75°) by expanding sin (30° + 45°) and simplifying with exact values. | Find the exact value of cos (105°) by expanding cos (60° + 45°) and simplifying with exact values. |
|
| Expand sin ((a+b) - c). | Expand cos ((3α + 2β)+ γ). | |
| Expand cos (2θ + 60°). | Expand tan (x + 135°). | |
| Simplifying. | cos 60°cos 30° - sin 60° sin 30°. | sin 60°cos 30° - cos 60° sin 30°. |
Simplify sin (2α + β) cosβ - cos (2α + β)sin (β) |
||
| Evaluating. | If where 0 < β < α < 90°, evaluate
|
|
| Equations. | (i) Show that
(ii) Hence find the solutions for tan 2x + tanx = 0 in the domain [0, 90°]. |
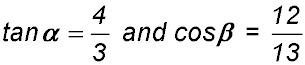 ,
,