Where the techniques of Maths
are explained in simple terms.
Trigonometric functions - Calculus - Differentiate ... hence find.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page all require you:
1. to differentiate the first equation/expression; and
2. to use the results of that differentiation to determine the integral of another.
| 1. (i) Differentiate x cosx.
(ii) Hence evaluate |
2. (i) Differentiate y = x2 + 1.
(ii) Hence find |
|
| 3. (i) Differentiate sinx - x cos x.
(ii) Hence find |
4. By differentiating y = cos x, find
|
|
| 5. | 6. | |
7. Use the trigonometry identity
|
8. (i) Differentiate y = x tan x. (ii) Hence find an expression for
(also using the results of Q7). |
|
| 9. (i) Differentiate
(ii) Hence find
|
10. (i) Differentiate cos2(3x) with respect to x.
(ii) Hence evaluate
|
|
| 11. | 12. | |
| 13. (i) Show that
tan3 x = tan x sec2 x - tanx (ii) Hence find |
14. | |
| Applications | 15. (i) Differentiate sin (x2).
(ii) Use this result to find the exact area bounded by y = xcos (x2), the x axis and the lines x = 0 and x = 1. |
|
16. (i) By expressing cot x as  prove that prove that 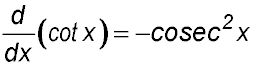 . .
(ii) Find the area of the region bounded by the curve y = cosec2 x, the x axis and the lines π/6 and x = π/3. |
||
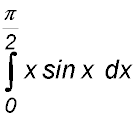 .
.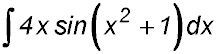 .
.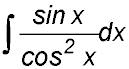 .
.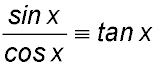 to show that
to show that 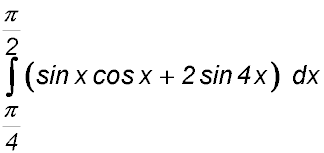 .
.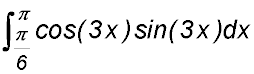 .
.