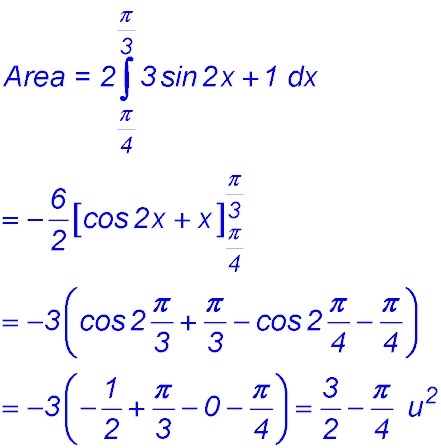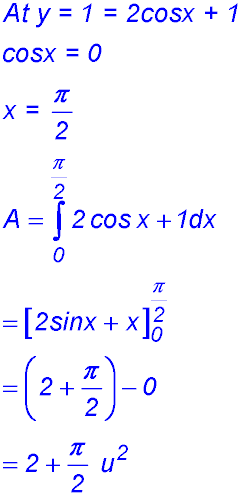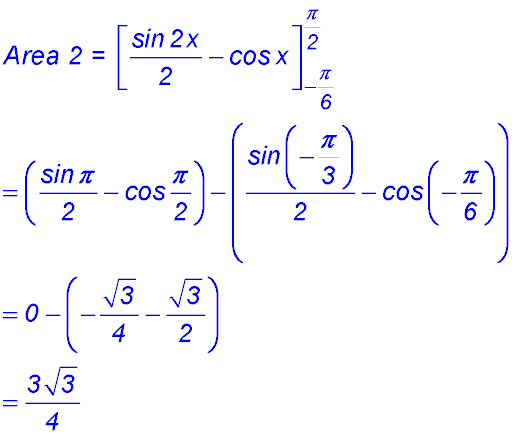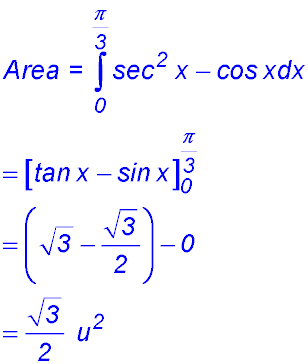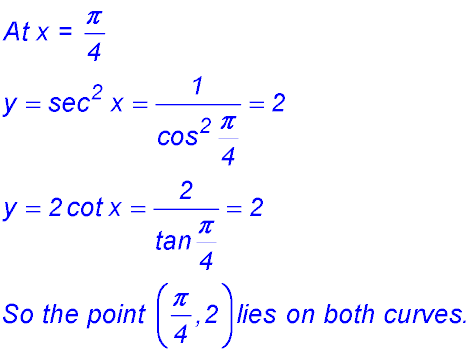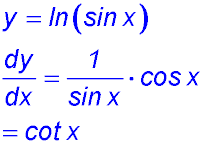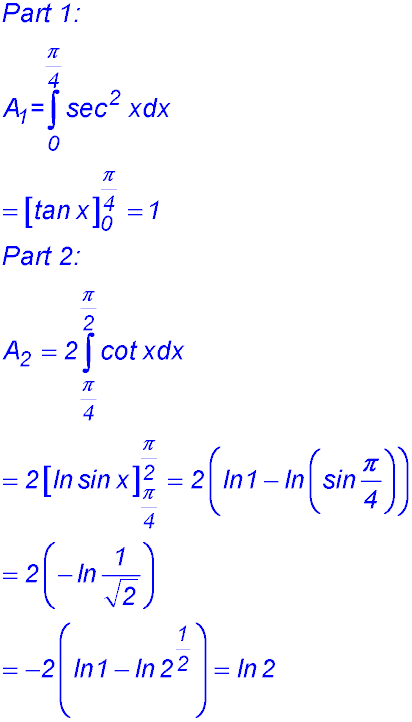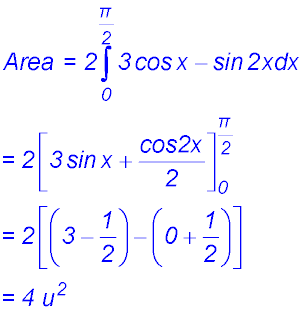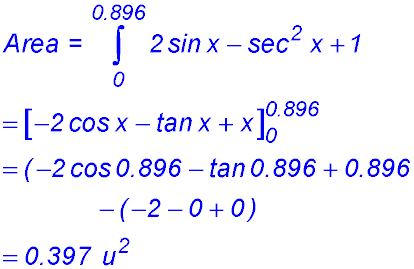Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Trigonometric functions - Integration - Applications finding areas.
Test Yourself 1 - Solutions.


 

Solve the following problems as indicated:

Area -
1 curve		 1.

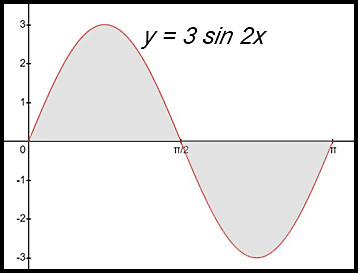
The curve is symmetrical about y = π/2. So the area between 0 and π/2 can be determined and then doubled.

 2. (i)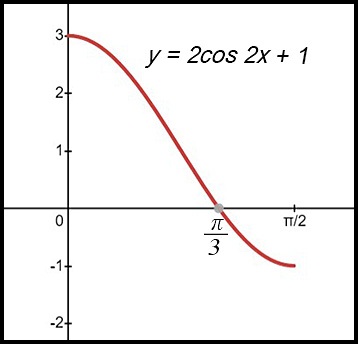

(ii) When y = 1:

1 = 2 cos2x + 1

cos 2x = 0

x = π/4

∴ There are two shapes:

1. a rectangle of height 1 and length π/4.

2. the area under the curve between π/4 and π/3.

For the 2nd area:
  3.

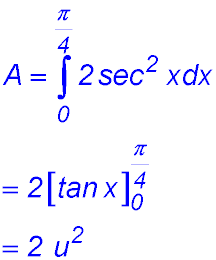4. (iii)
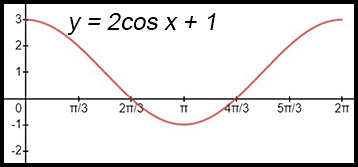
4. f(x) = 2cos x + 1,

(i) Range is [-1, 3]

(ii)

  5. (i)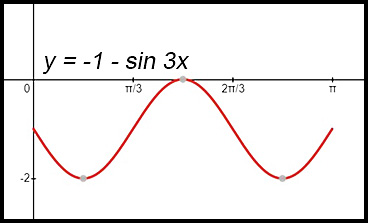

 

 (ii)
  6.

 
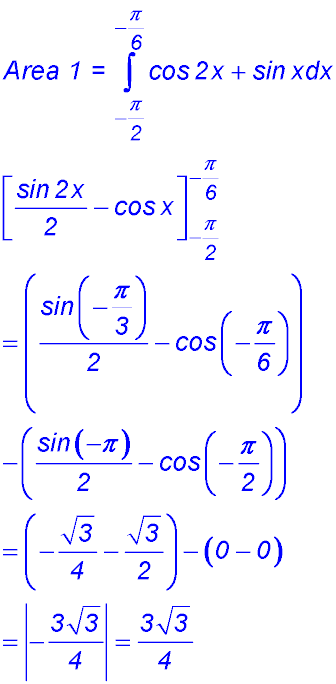  7. (i)

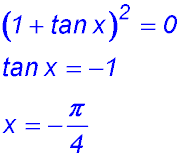
(ii)

x -π/3 -π/4 -π/6
f '(x)

8(1-√3)

< 0

 0

3(1 + 1/√2)

> 0

(iii)

(iv)

  8.  
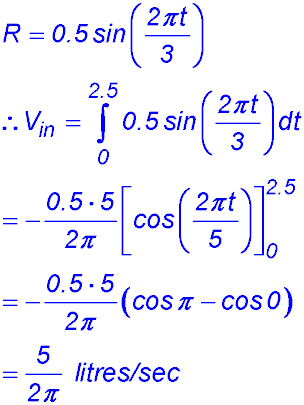Area -
2 curves with no point of intersection.		 9. (i)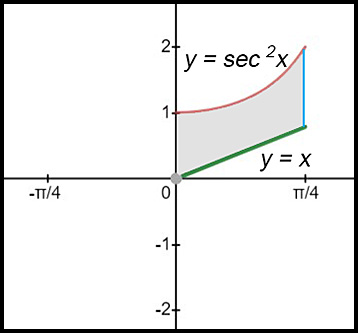

(ii)

10. (i)

(ii)

 
Area -
2 curves with one point of intersection		 11. 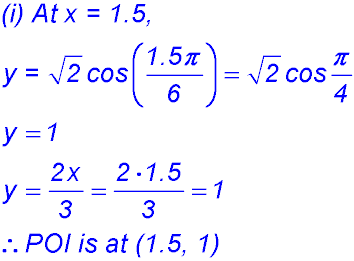(ii)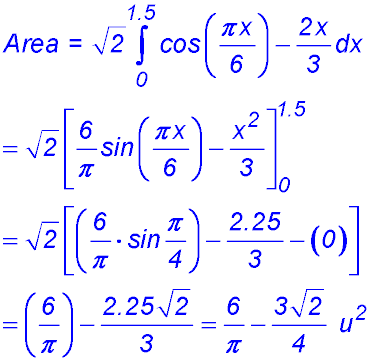
  12.

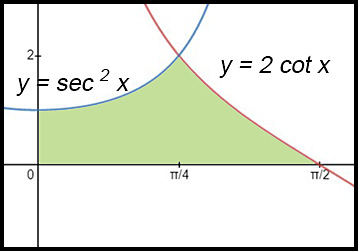
(i)

 

(ii)

(iii) There are two parts to integrate -

  • from 0 to π/4 under sec2 x; and
  • from π/4 to π/2 under 2 cot x.

∴ Area = 1 + ln 2 
  13. (i)

(ii) The two curves are symmetrical about x = π/2.

So areas are doubled to obtain total areas from
x = 0 to x = π.
  14. (i) 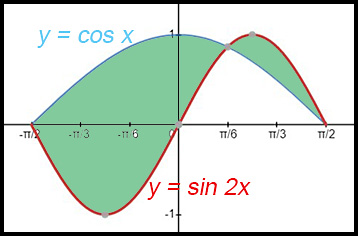(ii)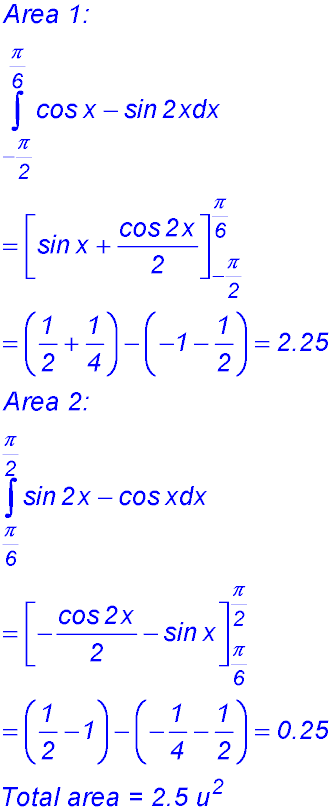
Area -
2 curves with two points of intersection		 15.

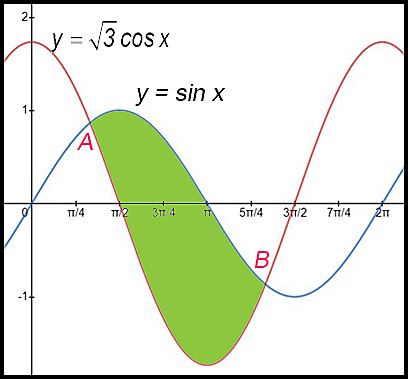
(i)

(ii)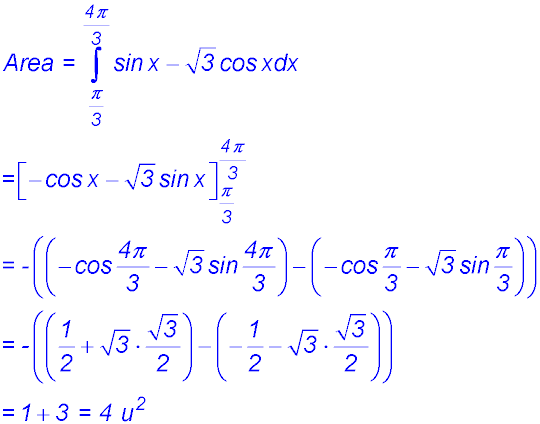
  16. (i)

x = 0, y = 2sin x = 2 sin 0 = 0

and y = sec 2x - 1 = (1/cos 20) - 1 = 0

x = 0.896, y = 2sin x = 2 sin 0.896 = 1.562

and y = sec 2x - 1 = (1/cos 20.896) - 1 = 1.562

Hence the curves intersect at x = 0 and
at x = 0.896 radians.

(ii)