Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.
Where the techniques of Maths
are explained in simple terms.
Trigonometric Functions - differentiation - Tangents, normals and other.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Solve the following problems - leave your answer in exact form unless otherwise indicated:
| Tangents | 1. Find the equation of the tangent to the curve y = sin 3x at 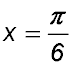 . .
Answer.y = -3x + π. |
2. Find the equation of the tangent to y = sec x at |
3. Find the equation of the tangent to y = 3 sin 2x + x - 2 at 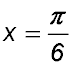 . . |
4. A curve has the equation
y = x cos x Given that P |
|
5. Find the equation of the tangent to y = 3 cosecx + 1 at 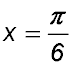 . . |
6. Find the equation to y = sinx + cos x at 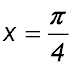 . .
Answer.y = √2. |
|
| Normals | 7. Find the equation of the normal to the curve y = sin 2x at the point (π/2, 0). |
8. Develop the equation of the normal to the curve
y = x sin x where x = π/2. Answer.y = -x + π. |
9. Find the equation of the normal to y = 2 sin 2x + 3 at the point where 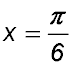 . . |
10. (i) Find the equation of the normal to y = e cosx at x = π.
(ii) Determine the length of the normal to the curve from the point on the curve where x = π to the point where the normal crosses the x axis. |
|
11. Prove that the normal to y = x tan x at 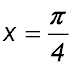 cuts the x axis at approximately x = 2.8.
cuts the x axis at approximately x = 2.8. |
12. Find the x values of the points on y = 3cosx + √2 (x) where the normal has a gradient which is undefined is the domain [0, π]. Answer. |
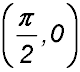 is the first point to the right of the origin where the curve crosses the x axis, find the equation of the tangent
is the first point to the right of the origin where the curve crosses the x axis, find the equation of the tangent