Where the techniques of Maths
are explained in simple terms.
Trigonometric functions - Graphing and interpretation.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Given an equation, describe the features (include references to shifts and dilations). |
1. Describe the main features for the curve y = 3cos 2x. |
| 2. Describe the main features for the curve y = 2 + sin x. | |
| 3. Describe the main features for the curve y = 2 - 3 cos 4x. | |
4. Describe the main features for the curve 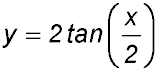 . . |
|
| 5. Describe the main features for the curve
|
|
| Given a graph, interpret the features (include references to shifts and dilations). |
6. The graph above can be represented by an equation of the form Find the values of a and n. Answer.a = 2 and n = π/2. |
| 7. The equation of the following graph is written in the form y = A + B cos(Cx - D). Determine the values of A, B, C and D. Answer.A = 4, B = 2, C = 1 and D = 0. |
|
| 8. The equation of the following graph is written in the form y = A + B tan(Cx + D). Determine the values of A, B, C and D. Answer.A = 0, B = 3, C = 2 and D = 0. |
|
| 9. The equation of the following graph is written in the form y = A + B sin(Cx + D). Determine the values of A, B, C and D. Answer.A = 3, B = 2, C = 1 and D = -π/3. |
|
10. The graph of D = A + Bcos Ct is given below.
Answer.A = -3, B = 2, C = π. |
|
| 11. What is the equation for the curve shown in the diagram below? Explain your reasons for your answer. |
|
| Sketch graphs with transformations. | 12. Sketch y = cos t + 2 for t:[0, 2π]. |
13. For the function y = 2 cos x
|
|
14. For the function y = -2 sin 3x;
|
|
15. Draw sketches, on the same axes, of the curves
 in the domain in the domainof x:[0, 4]. |
|
| 16. Sketch the curve y = 1 - 2 sin 2t for 0 ≤ t ≤ 2π. | |
| 17. Sketch the curve y = -3 + 2 cos πt for 0 ≤ t ≤ 2π. | |
| 18. Sketch the curve y = 2 + 3tan 2t for -π ≤ t ≤ π. | |
| 19. Sketch the curve y = 2 - 3 sin (t - |
|
| 20. (i) Sketch the graph of y = 1 - 2cos x for 0 ≤x ≤ 2π. Clearly indicate the end points of the curve in its given domain as well as its turning points. (ii) Use your graph to solve 1 - 2cos x = 0 in the given domain. |
|
| 21. (i) Sketch the curves y = sin x and y = cos x on the same axes for 0 ≤ x ≤ 2π.
(ii) By adding ordinates, develop the graph of y = sin x + cos x. |
|
| Graphs of reciprocal functions. | 22. Sketch the curve y = 2 cosec 2x for 0° ≤ x ≤ 360°. |
| 23. Sketch the curve y = cot 2t for 0° ≤ t ≤ 360°. | |
| 24. Sketch the curve y = sec x + 2 for 0 ≤x ≤ 2π. | |
| 25. Sketch the curve y = sec2 x for 0 ≤x ≤ 2π. | |
| 26. Sketch the curve y = 2 cot2 t for -π ≤ t ≤ π. | |
| 27. Sketch the curve y = 2 - cosec x for -3π/2 ≤ x ≤ 3π/2. | |
| Given features, draw the graph. | 28. Draw a sine graph which has a maximum value of 7 and a minimum value of 1 and has two patterns in its domain of 0 ≤x ≤ 2π. |
| 29. Draw a tan graph using the domain 0 ≤x ≤ 2π with the function having consecutive values of 0 at x = 0 and at x = π/4 and also a value of 5 at
x = π/8. |
|
| 30. Draw a sec graph which has minimum values of 2 at t = 0 and at t = 2π and a maximum value of -2 at t = π. Use the domain of -2π ≤ t ≤ 2π. |
|
| 31. Draw a cosine graph having a minimum value of -4 at x = 0, a maximum value of 0 and having two patterns in its domain of 0 ≤x ≤ 2π. |
|
| Determining the number of solutions. | 32. (i) Sketch the graph of y = 2cos 2x for -π ≤ x ≤ π.
|
| 33. (i) Sketch the graphs of y = 3 cos 2θ and y = 1 for 0 ≤ θ ≤ π.
(ii) Use your graphs to obtain two approximate solutions to the equation. (iii) Solve the equation 3 cos 2θ = 1 using the normal technique for 0 ≤ θ ≤ π (answer to 3 decimal places) and compare your answers with those in part (ii). |
|
34. (i) Sketch y = tan πx for 0 ≤ x ≤ 2.
|
|
35. (i) Sketch the graph of y = sin 2x for 0 ≤ x ≤ π using relevant sub-intervals.
|
|
| 36. (i) Draw a neat sketch of the curve y = 3sin 2x for 0 ≤ x ≤ 2π.
|
