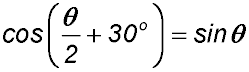Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.
Where the techniques of Maths
are explained in simple terms.
Trigonometry - Solving equations.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Make sure you have read the page titled Trigonometric Equations - summary of strategies.
| The questions below focus on the formats: |
| 1. Trig ratio and a constant. |
| 2. Squared trig ratio and a constant. |
| 3. Sin and cos terms but no constant. |
| 4. Trig ratios in a quadratic format. |
| 5. Using angles of any magnitude. |
| 6. Number of solutions. |
| 1. Trig ratio and a constant.
(solve all equations for |
1. Answer.150°, 330°. |
2. sec x = 2. Answer.60°, 300°. |
| 3. Solve Answer.240°, 300°. |
4. Solve sin 2x = 1. Answer.45°, 225°. |
|
| 5. Solve for 0 ≤ x ≤ 2π. Answer.5π/12, 7π/12, 17π/12, 19π/12. |
6. sin (x - 25°) = 0.5. Answer.55°, 175°. |
|
| 7. Answer.60°, 120°. |
8. 2cos θ = -1.
Answer.120°, 240°. |
|
| 9. tan θ = -0.8391 for -180° ≤ θ ≤ 180°. Answer.140°, -40°. |
10. cos (x - 35°) = -0.5 for -180° ≤ θ ≤ 180°. Answer.155°, -85°. |
|
| 2. Squared trig ratio and a constant. | 11. 3tan2 β - 1 = 0
Answer.β = 30°, 150°, 210°, 330°. |
12. 4cos2 x - 1 = 0
for -180° ≤ θ ≤ 180°. Answer.x = -120°, -60°, 60°, 120°. |
| 13. Answer.x = 15°, 165°, 195°, 330° 195°, 255°, 285°, 345°. |
14. sin2 x = 1
Answer.x = 90°, 270°. |
|
| 15. Answer.x = 30°, 60°, 120°, 150° 210°, 240°, 300°, 330°. |
16. 4cot2 (x + 30°) - 12 = 0.
Answer.x = 0°, 120°, 180°, 270°, 360°. |
|
| 3. Sin and cos terms but no constant. | 17. Answer.α = 30°, 210°. |
18. Answer.x = 0°, 120°, 180°, 300°. |
| 19. Answer.26° 34', 206° 34. |
20. 2sinθ cosθ = sin θ.
Answer.0°, 63° 26', 180°, 246° 26', 360°. |
|
| 4. Trig ratios in a quadratic format. | 21. Find the exact solutions for θ given the equation
2sin2 θ - sin θ - 1 = 0 (0 ≤ θ ≤ 360°).Answer.180°, 210°, 330°. |
22. Solve for θ:
2cos2θ + 3sinθ cosθ + sin2θ = 0 (0 ≤ θ ≤ 360°).Answer.135°, 315°, 153°26', 333°26'. |
| 23. (i) Show that
(cosec2 A - 1)sin2 A = cos2 A (ii) Hence or otherwise solve (cosec2A - 1)sin2A = 0.75 for -π ≤ A ≤ π Answer.π/6, 5π/6, 7π/6, 11π/6. |
24. Solve for θ:
8cos2x = 2sinx + 7 (0 ≤ θ ≤ 360°) Answer.210°, 330°, 14°29' or 165°31'. |
|
| 25. Solve the equation
cos2x + sinx + 1 = 0 (0 ≤ θ ≤ 360°).Answer.0°, 90°, 180°. |
26. Solve the equation
2 cos2J - 5sin J + 1 = 0 for 0 ≤ J ≤ 360°.Answer.270°. |
|
| 5. Complementary or supplementary angles.
(0 ≤ θ ≤ 360°). |
27. Solve:
|
28. cot (90° - 5x) = tan (3x + 36°)
Answer.x = 18°. |
| 29. sin (180° - 3x) = cos (5x-22°). Answer.x = 14°. |
30. 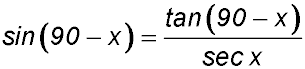
Answer.x = 45°, 224°, 90°, 270°. |
|
| 6. Number of solutions. | 31. How many solutions are there for the equation
(2cos 2x - 1)(sin2 x + 1) = 0 |
32. How many solutions are there between 0 and 2π for the equation (sin x - 1)(tan x + 2) = 0
Answer.2 solutions. |
| 33. How many solutions are there for the equation
(cos θ + 1)(cosec θ - 1) = 0. (θ = π/2 but ≠ π). |