Probability - discrete expected TYS 1

Calculate mean (expected value).

x	0	1	4	9	16
Pr (X=x)	0.1	0.2	0.4	0.2	0.1

E(x)= 0(0.1) + 1(0.2) + 4(0.4)
+ 9(0.2) + 16(0.1)

= 5.2

x	0	1	2	3	4
Pr (X=x)	0.05	0.2	0.3	0.4	0.05

Expected number of cars expected in 10 mins:

E(x)= 0(0.05) + 1(0.2) + 3(0.4) + 4(0.05) = 2.2 cars.

3. (i) Summarise the information in a probability distribution table.

x $0 $25 $200

Pr (X=x) 495/500 4/500 1/500

(ii) find the expected value of the winnings for each ticket.

E(x) = 0(0.99) + 25(0.05) + 200(0.002) = $1.65.

4. The probability distribution can be written as:

x	0	1	2
Pr (X=x)	0.5	0.3	0.2

Expected number of books purchased = 0(0.5) + 1(0.3) + 2(0.2) = 0.7.

5. The probabiity distribution for the gold can be written as:

X	Pr (X=x)
$500	0.4
$400	0.5
$200	0.1

(i) E(X) = 0.4(500) + 0.5(400) + 0.1($200) = $420.

So if the best option happened, the gold coin is worth less than $450.

(ii) If the probabilities were altered to

X	Pr (X=x)
$500	0.7
$400	0.2
$200	0.1

the expected value of the prize would equal $450. There would also be other ways

(Note: having the probabilities in your calculator makes changing values for this search much easier).

6. (i)

% profit	20%	10%	-15%
p(X)	0.20	0.50	0.30

E(profit) = 20%×0.2 + 10%×0.5 - 15%× 0.3 = 0.045

so Expected % profit is 4.5%.

(ii) Expected profit on an investment of $2,400 = 2400×4.5% = $108.

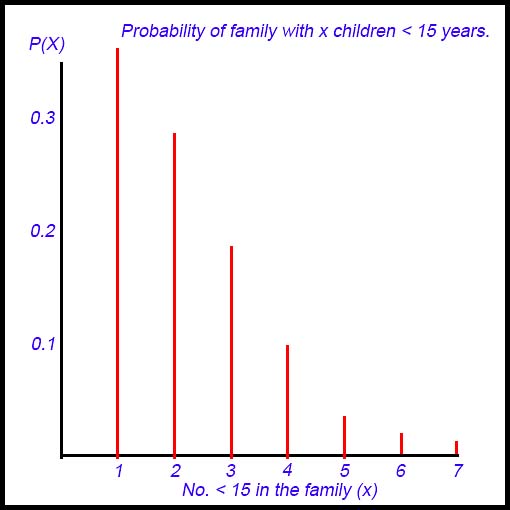
7. (i)

(ii) "Most likely number" is the Expected Number:

E(x) = 1×0.351 + 2×0.294 + 3×0.194 + ...+ 7×0.009 = 2.26 children

(iii) P(<4 children) = 0.351 + 0.294 + 0.194 = 0.839.

(iv) P(> 5) = 0.014 + 0.009 = 0.023.

Calculate standard deviation.

8. Variance = 52 - 6² = 16.

Standard deviation = 4.

9. Variance = 565 - 22² = 81.

Standard deviation = 9.

10. If E(X²) = 25 and SD = 3.

3² = 25 - (E(X))²

E(X) = 4.

Calculate both the mean and the standard deviation.

11.

X	0	1	2	3	4
p(x)	0.1	0.2	0.4	0.2	0.1
X²	0	1	4	9	16

E(X) = 0×0.1 + 1×0.2 + 2×0.4 + 3×0.2 + 4×0.1 = 2

E(x²) = 0×0.1 + 1×0.2 + 4×0.4 + 9×0.2 + 16×0.1 = 5.2

Var (X) = E(x²) - [E(X)]² = 5.2 - 2² = 1.2.

12.

X	1	2	3	4
P(X)	0.3	0.45	a	b
X²	1	4	9	16

(i) As a pdf, the sum of the probabilities is 1.0.

Hence 0.3 + 0.45 + a + b = 1

a = 0.25 - b

E(X) = 2 = 1×0.3 + 2×0.45 + 3a + 4b

3a + 4b = 0.8

Substituting:

3(0.25 - b) + 4b = 0.8

b = 0.05

a = 0.20

(ii) E(X) = 1×0.3 + 2×0.45 + 3×0.2 + 4×0.05 = 2 (as given)

E(X²) = 1×0.3 + 4×0.45 + 9×0.2 + 16×0.05 = 4.7

Var (X) = E(x²) - [E(X)]² = 4.7 - 2² = 0.7.

SD = 0.84.

13.

X	1	2	3	4
X²	1	4	9	16
p(x)	0.4	0.3	0.2	0.1

(i) E(x) = 1(0.4) + 2(0.3) + 3(0.2) + 4(0.1) = 2.0

E(x²) = 1(0.4) + 4(0.3) + 9(0.2) + 16(0.1) = 5.0

Var (x) = 5 - 2² = 1

(ii) Is E(X) a possible value of X? Yes

14. X is a random variable with the following probability distribution:

X	5	10	15	20	25
p(x)	0.05	0.30	0.25	0.25	0.15
X²	25	100	225	400	625

μ = E(x) = 5(0.05) + 10 (0.30) + 15(0.25) + 20 (0.25) + 25 (0.15)

= 15.75

E(X²) = 25(0.05) + 100 (0.30) + 225(0.25) + 400 (0.25) + 625 (0.15)

= 281.25
σ = √(281.25 - 15.75²) = 5.76

15.

X (no of visits)	0	1	2	3
P(x)	0.10	0.30	0.40	0.20
X²	0	1	4	9

(i) Mean: 0×0.1 + 1×0.3 + 2×0.4 + 3×0.2 = 1.7

E (X²) = 0×0.1 + 1×0.3 + 4×0.4 + 9×0.2 = 3.7

Var (X) = 3.7 - 1.7² = 0.81.

Standard deviation = 0.9

(ii) Probab (at least twice) = 0.4 + 0.2 = 0.6

(iii) Pr (X ≤ 1.5) = 0.1 + 0.3 = 0.4

(iv)

16. (i) E(X) = 1×(1/9) + 2×(2/9) + 3×(1/9) + 4×(2/9) + 5×(1/9) + 6×(2/9)

= 11/3 = 3.67

E (X²) = 1²×(1/9) + 2²×(2/9) + 3²×(1/9) + 4²×(2/9) + 5²×(1/9)
+ 6²×(2/9) = 49/3 = 16.33

Var (X) = 16.33 - 3.67² = 2.86
(or 49/3 - (11/3)² = 26/9 = 2.88 using the fractions)

(ii) If each roll has an expected value of 3.67, we would need

100 ÷ 3.67 = 27.2 rolls - hence 28 rolls to exceed 100.

17.

No of goals	0	1	2	3
Tracey (N)	4	5	0	6
Tracey (prob)	0.27	0.33	0	0.40
Alyssa (N)	2	7	1	5
Alyssa (prob)	0.13	0.47	0.07	0.33

(ii) Tracey:

E(X) = 0×0.27 + 1×0.33 + 2×0 + 3×0.40 = 1.53 goals

E(X²) = 0×0.27 + 1×0.33 + 4×0 + 9×0.40 = 3.93

Var (X) = 3.93 - 1.53² = 1.6

Alyssa:

E(X) = 0×0.13 + 1×0.47 + 2×0.07 + 3×0.33 = 1.60 goals

E(X²) = 0×0.13 + 1×0.47 + 4×0.07 + 9×0.33 = 3.72

Var (X) = 3.72 - 1.60² = 1.16.

Alyssa may be slightly the better player. She has a slightly better average and the variability of her scoring is smaller.

18. Jamie's probability distribution is:

No. of red cards face-up	0	1	2	3	4
Probability	0.03	0.40	0.30	0.26	0.01
N²	0	1	4	9	16

(i) Expected number = 0 + 1(0.40) + 2(0.30) + 3(0.26) + 4(0.01)

= 1.82 red cards

(ii) E(X²) = 0 + 1(0.40) + 4(0.30) + 9(0.26) + 16(0.01) = 4.1

∴ Variability = √(4.1 - 1.82²⁾ = 0.89

19. The probability distribution of the number of butterflies in a garden at 10:00 am each morning is p(X):

No. of B/f	0	1	2	>2
Pr (B/f=x)	0.5	0.3	0.2	0.0

(i) Expected number of butterflies = 0(0.5) + 1(0.3) + 2(0.2) + 0

= 0.7.

(ii) E(X²) = 0 + 1(0.3) + 4(0.2) + 0 = 1.1

SD = √(1.1 - 0.7² = 0.78.

20. (i) The sum of the 4 probabilities must = 1.

∴ k + 3k + k + 3k = 1

k = 1/8 or 0.125

(ii)

X = x	1	2	3	4
P(X)	0.125	0.125	0.375	0.375

(iii)

X = x	1	2	3	4
P(X)	0.125	0.125	0.375	0.375
x²	1	4	9	16

Var (X) = E(X²) - (E(X))² = 10 - 3² = 1

21.

No. of pairs of pigeons	4	5	6	7	8
Pr (pigeon)	0.1	0.1	0.4	0.2	0.2
Pairs²	16	25	36	49	64

(i) Expected pairs = 4×0.1 + 5×0.1 + 6×0.4 + 7×0.2 + 8×0.2 = 6.3

So I can expect to see 6 pairs of Crested Pigeons.

(ii) E(x²) = 16×0.1 + 25×0.1 + 36×0.4 + 49×0.2 + 64×0.2 = 41.1

Hence Var(x) = 41.1 - 6.3² = 1.41.

So not much variation from day to day.