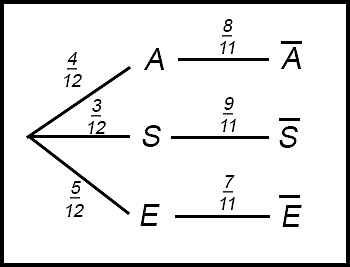
1. We could draw a tree but not essential in this question for the first 2 parts - up to you. Maybe safer if you are not sure.

There are 5 English speakers in the 12 students.

(i) both speak English.

(ii) neither speaks English;

There are 7 students who do not speak English.

(iii) they do not speak the same language.

Now we need a tree - but with a difference by combining groups.

The letter with the bar indicates "NOT THAT". So A with the bar conveys the meaning "not Arabic".

So multiplying across and adding down at the RH side:

2. The other five numbers can appear so the probability of the 6 not appearing in any one roll is 5/6.

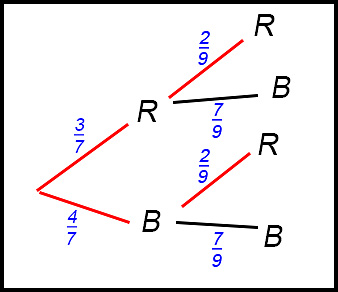
4.

(i) Probability of 2 red balls (taking the top all red route)

(ii) Probability of at least 1 red ball - so add 1 red to 2 red.

Start with finding about 1 red ball by following both the
RB and BR paths:

Now add the path in part (i)

(iii) Probability of at most one red - so add 1 red to 0 red (BB):

6.

(i) passes all three tests?

Check the blue line.

Prob (passes all 3) = 0.6 × 0.8 × 0.7 = 0.336.

(ii) passes exactly one of these tests?

Check the green lines.

Prob (passes one and fails 2) =
0.6 × 0.2 × 0.3 + 0.4 × 0.8 × 0.3 + 0.4 × 0.2 × 0.7 = 0.188

(iii) passes at least one of these tests?

Follow the red line.

Pr (passing ≥ 1) = 1 - Prob (failing 3)

= 1 - (0.4×0.2×0.3) = 0.976

6. A biassed coin is such that the probability of getting a head is 5/8. The coin is tossed twice.

(a) What is the probability of the result being:

(i) two heads?

(ii) two tails?

(iii) a head and a tail?

(b) If the first toss results in a head, what is the probability that the second toss will result in a tail?

(i) rain on any three consecutive days?

(ii) rain on all six weekend days in July?

(iii) one 5 day school week having rain only on Monday, Wednesday and Friday?

(iv) no rain during the 5 days of a school week?

(i) The probability that the first ball drawn is white.

(ii) The probability that the second ball drawn is white.

(iii) The probability that both balls are white.

(iv) The probability that at least one ball is white.

(i) The probability that the first ball drawn is white.

(ii) The probability that the second ball drawn is white.

(iii) The probability that both balls are white.

(iv) The probability that at least one ball is white.

12. Grace buys 4 tickets in a raffle. There is a total of 100 tickets being sold. The prizes on offer are $40 for first prixe,, $30 for second prize and $20 for third prize. Find the probability that Grace:

(i) wins $70.

(ii) wins $30.

(iii) wins a prize.

13. There are six balls in an urn. They are numbered with the digits 1 to 6. The balls are drawn one at a time.

What is the probability that:

(i) the ball with the number 3 is drawn first?

(ii) either the ball with the number 2 of the number 4 is drawn as the third ball?

(iii) the product of the numbers on the first two balls is 12?

14. NO = there are 7 black balls and 11 balls - so reduce each number and multiply.

(i) To select 2 green from Container 2, first select Container 1 (Prob = ½) then 1 green ball (Prob 4/11) then the second green ball (Prob = 3/10)

Multiply: .

(ii) Selecting at least one green uses the above result but also the two ways to get only one green from Container 2.

15. (i) Prob (Black) = 3/5.

(ii) As GGG is not possible, Prob (BBB) = .

(iii)

16. James hitting a moving target with an arrow at least once is to exceed 80%?

Probability of hitting the target more than once > 0.80
is the same as (1 - probability of missing every time).

Let the probability of missing every time (which is 0.8ⁿ) = 0.2
(so ignore the inequality for now).

∴ Taking logs: n = log_0.8 0.2 = 7.213.

Now to be less than the 20% chance of missing every time, James needs to shoot at least 8 arrows (because we just solved for equaling the 20%).

So 8 is the number of shots James must make to have his probability of hitting the target at least once greater than 80%.

A blue ball is selected from Bag A with a probability of 4/7. That outcome gives 3 blue balls and 3 red balls in Bag B. Hence the probability of picking a red ball with this composition is 1/2.
So the combination of these two probabilities for picking a red ball from Bag B is 2/7.

A red ball is selected from Bag A with a probability of 3/7. That outcome gives 2 blue balls and 4 red balls in Bag B. Hence the probability of picking a red ball with this composition is 2/3.
So the combination of these two probabilities for picking a red ball from Bag B is also 2/7.

Adding these independent outcomes give the probability of a red as 4/7.

Find the probability that an attacking player is tackled.

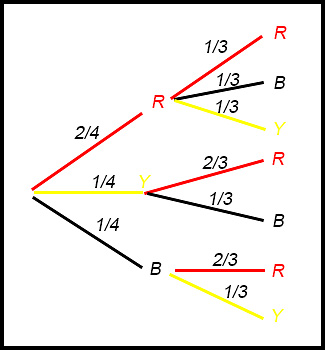
(i) What is the probability that both selected marbles are red?

Take the all red path:

Pr (RR) = 1/4 ×1/3 = 1/12.

(ii) Unfortunately one marble rolls away and everyone sees that it is black. What is the probability that the remaining hidden marble is red?

First go to any path with red-black combination. There are two such paths.

Multiplying the probabilities along these paths and adding, we get:

(2/4×1/3) + (1/4×2/3) = 1/3

Now go to the paths where there is a black. There are four paths:

Multiplying the probabilities along these paths and adding, we get:

2/4×1/3 + 1/4×1/3 + 1/4×2/3+1/4×1/3 = 1/2

Conditional probability asks "probability along paths with red" given "probability along paths with black"? Divide these two answers to obtain the probabilty of a red given a black has been seen. Probability = 2/3.

Alternatively, if a red is known to have been drawn, there are now 2 reds and a yellow left. So probability of a red = 2/3.
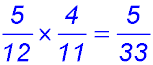
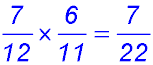
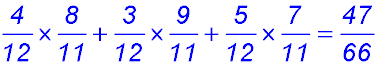
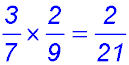
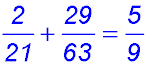
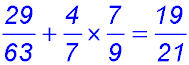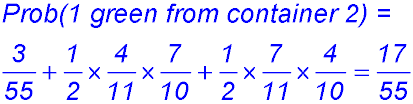