Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Normal distribution - z scores.
Test Yourself 1.


 

On this page, questions address:
1. Calculating each of the four important numbers.
2. Interpreting z scores.
3. Using z scores to combine your marks.
 

 

Calculating z scores. 1. 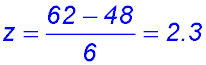2.
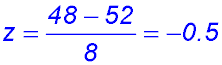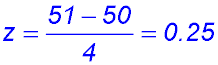
  3. 4.
Calculating the mean or the SD. 5.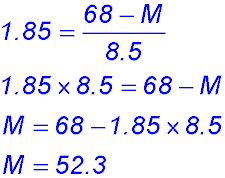
  6.
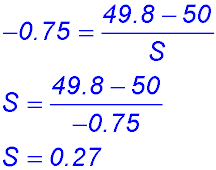  7.
  8.

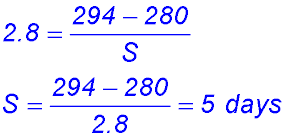
and official statistics show nearly 70% of babies are born between -5 and +5 days of the mean
Yea!! Go Charles.

  9. sdz=0
Calculating a value. 10.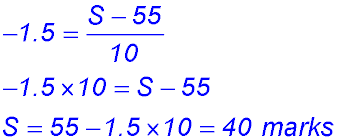
  11.
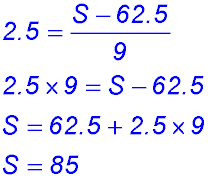  12.
  13.
  14.
Interpreting z scores.

15.
  17.
 
Answer.(i) 1 ≤ z ≤ 2.
(ii) % = 47.5% - 34% = 13.5%.
 

18.

 
Answer.(i) A z score of -1 means that the length of the component
is 10 - 0.02 = 9.98 cm.
(ii) A component in section A is between 10 and 10.02 cm
say 10.01 cm.
(iii) Number = 500 × (47.5%-34%)
= 500×13.5%
i.e. 68 components approx.
Using z scores to calculate total marks.

20. The table below contains marks obtained by Damien and Alyssa in their English and Mathematics assessments.

  Raw marks z scores
  Eng Maths Total Eng Maths Total
Alyssa 84 81 165 0.4 1.2 1.6
Damien 91 77 168 1.1 0.4 1.4
Mean 80 75        
Stand dev. 10 5        

When the raw marks are added - as almost every teacher does - variability within each group is not taken into account. It is easier, for eaxmple, to obtain better marks in subjects with high variablilty in marks as is shown by larger standard deviations. Such subjects have marks which are more "spread out".

If all subjects are deemed to be equal in value, the standard deviations should be the same. Hence when we equate the standard deviations with z scores, Alyssa turns out to be the better student. She scored better in Maths (which had the lower standard deviation). Hence when the two standard deviations are equated, Alyssa was the better student overall.

Ask your teachers to do this -:)
  21.
  22.