Where the techniques of Maths
are explained in simple terms.
Networks and Graph Theory - Minimum spanning trees.
Summary of steps for applying Prim's algorithm.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Prim's algorithm finds a minimum spanning tree for a connected weighted graph:
- starting with a given vertex;
- adding edges of increasing weight at each step;
- not all edges are used in a minimum spanning tree - just a subset of the edges in the network but every vertex in the network is used.
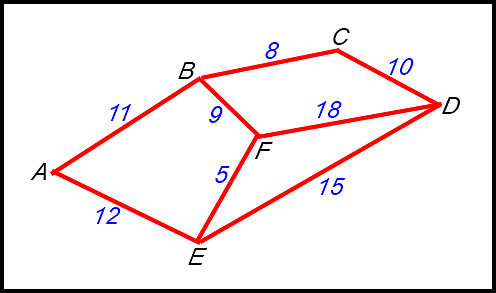
| Prepare a basis for the new network by copying the vertices into the approximate position they have in the original network diagram. | ||||||||||||||||||
| Step 1: | Our network begins at F - so we start there. | |||||||||||||||||
| Step 2: | List in a table, the edge weights to all vertices linked to the selected vertex F. |
|
||||||||||||||||
| Step 3: | Select the edge coming from vertex F with minimum weight (here FE) and draw it into your tree. | |||||||||||||||||
| Step 4: | Extend the list in your table with weights for all edges connected to the last selected vertex (E) but not yet included (here that will be EA and ED). Now look down the list for the minimum weight not included. We select FB. |
|
||||||||||||||||
| Step 5: | {Repeat steps 3 and 4 until all vertices are included}. Therefore add edges from B to the table (BA and BC). Select the lowest weight not yet used - which will be BC. Draw that into your diagram.
|
|
||||||||||||||||
Add edges from C to the table. The lowest unused weight in the list is now CD so draw that into your diagram. We cannot add more edges because all edges from D are already included (CD, DF and DE). Select the lowest weight not yet included - that will be BA. Add that to the diagram.
|
|
|||||||||||||||||
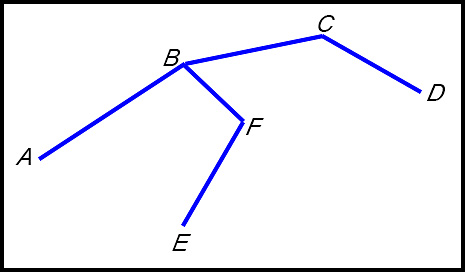
| All vertices are now included so we have our minimum spanning tree with a weight of 5 + 9 + 8 +10 + 11 = 43. | ||||||||||||||||||
 |