Where the techniques of Maths
are explained in simple terms.
Geometry - Circles - Mensuration.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| The questions on this page focus on: |
| 1. Arc length. |
| 2. Area of a sector. |
| 3. Area of a segment. |
| 4. Mixed questions. |
| The relevant formulae to use : | when the angle is given in degrees are |
when the angle is given in radians: |
| Arc length | 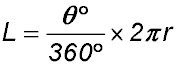 |
L = rθ |
| Area of a sector |  |
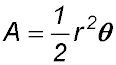 |
| Area of a segment | A = area of sector - area of triangle. | |
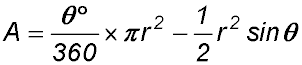 |
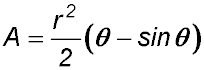 |
|
where:
|
where:
|
| Arc length, radius and angles. | 1. The angle subtended at the centre O of a sector is 42°.
The radius of the circle is 10 cm. Find the arc length to the nearest mm. Answer.7.3 cm. |
| 2. What is the length of the arc subtended by an angle of 120° in a circle of radius 26 m?
Answer.54.5 m. |
|
| 3. What is the length of the arc subtended by an angle of
|
|
4. The hour hand of a clock is 10 cm long.
Answer.26.2 cm. |
|
5. A train travels around a circular arc of radius 250 metres. It travels at a speed of 15 km/hour and it takes 30 seconds to complete this curve.
Answer.(i) At 250 m/min, distance = 125 m. (ii) θ = 0.5 rads. |
|
| 6. Compute the length (to the nearest metre) of the arc formed on Earth by 1 minute of change in the latitude.
Assume the radius of Earth is 6,400 km. |
|
| Find angle. | 7. A circle has radius of 5 cm. Find the size of the angle subtended at the centre of this circle by an arc of length 10 cm.
Answer correct to the nearest minute. Answer.Angle = 114° 35'. |
| 8. An arc of length 3.163 m is located on the circumference of a circle which has a radius of 12.6 m.
What angle (to the nearest minute) is subtended by this arc at the centre? Answer.Angle = 14° 23'. |
|
| Find radius. | 9. What is the radius of a circle (to the nearest cm) whose center angle of 98° subtends an arc on the circumference of 42 cm. Answer.Radius = 25 cm. |
| 10. An angle of 60° 22' subtends an arc of length 46 cm on the circumference of a circle.
What is the radius of the circle (nearest mm)? Answer.Radius = 39.7 cm. |
|
| 11. An angle of 2.3 radians subtends an arc of length 35 cm on the circumference of a circle.
Find the radius of the circle (nearest mm). Answer.Radius = 15.2 cm. |
|
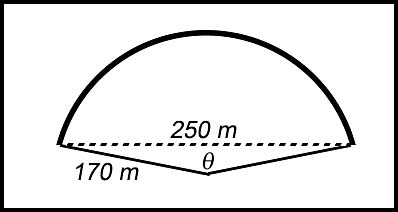
| Miscellaneous. | 12. A straight road was constructed to cut out a dangerous bend on a country road. Engineers had previously designed the bend to be part of an arc of radius 170 m. The new straight road is to have a length of 250 m.
Answer.(i) 95°. (ii) Shortened by 32 m (282 - 250 m). |
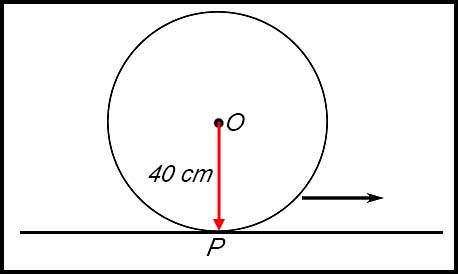
| 13. A wheel of radius 40 cm and centre O rolls along a horizontal path as shown below.
P is the point of contact between the wheel and the path before the wheel starts to roll. Hint:Always be careful with units. Answer.(i) Angle = 143°14'. (ii) Height = 40 + 32 = 72 cm. |
|
| Area of a sector | 14. The area of a sector is 10π units2 while the angle at the centre of the circle is 45°.
Find the exact value of the radius of the circle. AnswerRadius = 4√5 cm. |
| 15. AOB is the sector of a circle with centre O and radius r. < AOB = θ. The area of the sector is 20π cm2 and the length of the arc AB is 2π cm.
Answer(i) Radius = 20 cm. (ii) Angle = 17° 46'. |
|
16. A 10 cm arc on a circle subtends an angle of π/4 at the centre.
Answer(i) Radius = 40/π (ii) Area = 1400/π. |
|
17.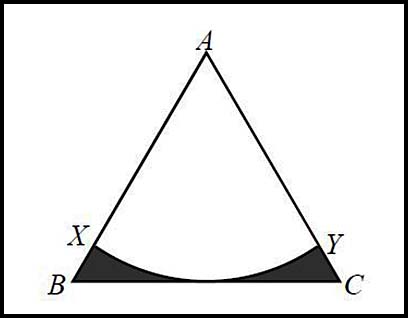
In the diagram, △ ABC is an equilateral triangle with sides of length 6 cm. An arc with centre A and BC as tangent, cuts AB and AC at X and Y respectively. Answer.(ii) Area = 9(√3 - π/2) cm2. | |
| Mixed exercises | 18. The circle shown in the diagram has a center at O and a radius of 70 cm. The length of the arc AB is 30 cm.
|
| 19. The length of an arc is 8 cm and the area of the sector is 25 cm2 when an angle of θ is subtended at the center of the circle. Hint.Great question for learning technique. Write out the two equations for Arc Length and for Area of the sector. We have simultaneous equations with the angle and the radius as unknowns. DIVIDE the area equation by the arc length equation to isolate radius. Then substitute to find the angle. REMEMBER THIS approach for a number of topics especially series!!! Answer.(i) radius = 6.25 cm; θ = 1.28 rads. (ii) Chord is 7.5 cm. |
|
| 20. A circle with center at O has a radius of 6 cm.
The area of a sector AOB in the circle has an area of 27 cm2. Answer.(i) Angle AOB = 86° or 1.5 rads. (ii) Arc length AB = 9 cm. |
|
| 21. From a circle with centre O, a sector OXY is cut out. The sector has radii of OX = OY = r cm.
The angle subtended at the centre <XOY = θ radians where Answer.(ii) As r = 15 cm, XY = 15√3 cm. |
|
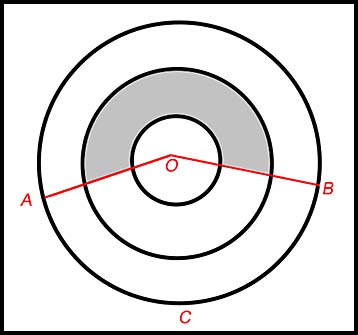
| 22. A set of three concentric circles with centre O and radii 3.5 cm, 9 cm and 12.5 cm is shown in the diagram below. The length of arc ACB is 22.5 cm
Answer.(i) Angle AOB = 4.483 rads. (ii) Area = 154 cm2. |