Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Quadratics - the Discriminant.
Test Yourself 1.


 

To answer the following questions - you will need to use the discriminant:

  1. to calculate the value of the discriminant;
  2. to interpret the value directly;
  3. to find values.
No real roots. 1. Show that the equation
x2 + 5x + 8 = 0 has no real roots.		 2. Show that the equation
2x2 - 12x + 25 = 0 has no real roots.
  3. For what values of p will the quadratic equation

x2 + (p - 2)x + 1 = 0

have unreal roots?

 4. Explain why the graph of the parabola described by the equation

y = 3x2 - 2x + 4

is located above the x axis for all values of x.
Real roots 5.For what value of m are the roots of f(x) = mx2 + 6x - 3 real?

 

 6. (i) Find the discriminant of the equation 3x2 + 2k + k = 0.

(ii) For what values of k does the equation
3x2 + 2k + k = 0 have real roots?

 
  7. Show that x2 + kx + k - 1 = 0 has real roots for all values of k. 8.
One real root 9. Find the value(s) of k for which the quadratic equation

3x2 + 2x + k = 0 has one real root.

Answer. k = 1/3.		 10. Find the values of k for which the quadratic equation
x2 - (k + 4)x + (k + 7) = 0 has equal roots.
Answer. k = -4 or k = -8.
  11. For what value(s) of k does the equation y = x2 - 2kx + 6k have
one real root?
Answer. k = 0 or k = 6.		 12.

 
Real and different roots. 13. Find the value(s) of k if the roots of the equation
x2 + kx + 36 = 0 are real and distinct.

14.
  15. For the quadratic equation

x2 + (p - 3)x - (2p + 1) = 0

(i) Show that the value of the discriminant can be expressed as
p2 + 2p + 13.

(ii) Hence or otherwise show that the quadratic equation above will always have real, distinct roots for real valued p.

 16.
Mixed questions. 17. For what values of k does

x2 - (k + 5)x + 9 = 0

have

(i) equal roots

(ii) no real roots.

 
Positive definite. 19. For what values of k is the equation kx2 - (k + 1) - 2k + 3 = 0 positive definite? 20. For what values of k is the equation

(k + 1) x2 - 2(2 + k) + 3 = 0

positive definite?


Answer. 4 - 2√6 < k < 4 + 2√6.
  21.  
Negative definite. 23.

 
  25. 26.
Advanced contexts. 27. (i) Show that for all values of m, the line y = mx - 3m2 touches the parabola x2 = 12y.

(ii) Find the values of m for which this line passes through the point (5,2).

(iii) Hence determine the equations of the two tangents to the given parabola from the point (5,2).

 

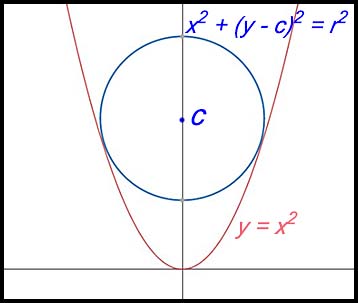
 28. The circle x2 + (y – c)2 = r2, where c > 0 and r > 0, lies inside the parabola y = x2. The circle touches the parabola at exactly two points located symmetrically on opposite sides of the y-axis, as shown in the diagram.

(i) Show that 4c = 1 + 4r2

(ii) Deduce that c > ½.
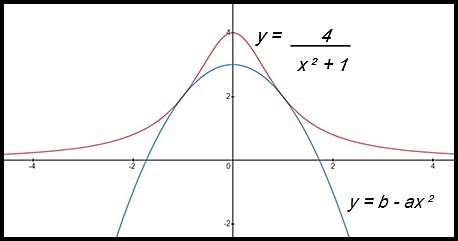
  29. The parabola y = b - ax2 , where a > 0 and b > 0 , is under the curve .

The parabola touches the curve at two points that are symmetrical at the y-axis, as shown in the diagram above.
Let the two curves intersect at x = ± q.

(i) Show aq4 + (a - b)q2 + 4 - b = 0
(ii) Hence show that .
(iii) Hence show 0 < a < 4.
  30. (i) Write down the discriminant of 2x2 + (k –2)x + 8, where k is a constant.

(ii) Hence, or otherwise, find the values of k for which the parabola
y =2x2 + kx + 9 does not intersect the line y =2x +1.

 
Increasing functions. 31. For what values of k is the curve y = x3 - 3x2 + kx + 3 always an increasing function?
  32.
Decreasing functions. 33.
  34.