Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Quadratics - the Discriminant - advanced applications.
Test Yourself 1.


 

Answer the following questions - you will need to use the discriminant:

Identification of tangents etc. 1.
  2.
  3. Given that the line lx + my + n = 0 is a tangent to

x2 = 4ay, prove .
  4.
  5. A parabola whose equation is y = kx2 (where k is a constant) has the line y = -6x + 3 as a tangent.

(i) By equating the two given equations, find a quadratic equation in terms of x and k.

(ii) By using the discriminant of the quadratic equation found in (i), find the value of k.

(iii) Find the coordinates of the point of contact between the tangent and the parabola.

(iv) Sketch the parabola and the tangent line, showing the coordinates of the point of contact and where the tangent line cuts the x and y axes.

Answer.(i) kx2 + 6x - 3 = 0
(ii) k = -3
(iii) Point of contact (1, -3).
  6
 
 
Nature of roots. 15. Show that the constants k and l have different signs if the quadratic equation

has no real roots .

  16. (i) For what values of k does the quadratic equation

kx2 + (k + 3)x - 1 = 0

have real roots?

(ii) Why cant the equation ever be positive definite?

 

Show that the quadratic equation

(a2 - b2)x2 + 2b(a - c)x + (b2 - c2) = 0

has real and rational roots for all values of x if a, b and c are rational.
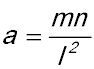