Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Functions - non-linear - Quadratics.
Comparison between a Parabola and a Catenary.



There is another curve to mention in passing.

It is the CATENARY curve. Its equation is .

It looks like a parabola, feels like a parabola - but it is not a parabola.

The graph to the right shows that, while the parabola and the catenary pass through four points in common (± 1.62, 2.63)
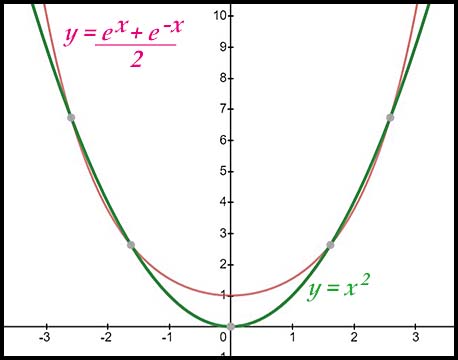and (± 2.59, 6.73), the parabola is not as wide as the catenary (except between the points of intersection). Clearly also the vertices are different.

We do not need much consideration of the catenary in this website at present. Suffice it to show three examples of every-day situations in which we see a catenary and not a parabola.


Chains follow the path of a catenary -
even those which are suspended in streets
and pedestrian malls.
Power lines - like these in the Oklohama Panhandle- suspended
between poles of big structures
trace out a catenary form

Many suspension bridges - like the Wakato Bridge in Fukoka, Japan - show a catenary in their curve - although this path sometimes converts to a parabola when the bridge is under load.

 

A good reference showing how a catenary curve in engineering can become a parabola was posted by Weimeng Lu.
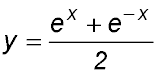