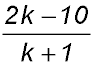Where the techniques of Maths
are explained in simple terms.
Linear functions - Testing for properties of lines.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
On this page, questions about properties involve:
| Parallel lines - | Lines which are parallel have the same gradient. |
| Testing gradients. | |
| Determining equations. | |
| Perpendicular lines - | Lines which are perpendicular have a gradient which is the negative inverse (i.e. turn the gradient of a given line upside down and change its sign). |
| Testing gradients. | |
| Determining equations. | |
| Collinear points. | Three or more points which lie on the same straight line. |
| Concurrent lines. | Three or more lines which all pass through the same point. |
| Parallel lines - testing gradient. | 1. Are the lines 2x + y - 6 = 0 and 4x + 2y + 6 = 0 parallel?
Answer.Both lines have the gradient of -2. ∴ parallel. |
2. Are the lines y = 4x + 23 = 0 and 16x - 4y + 3 = 0 parallel? Answer.Both lines have the gradient of 4 ∴ parallel. |
| 3. Are the lines y = 2x + 3 and y = -2x + 3 parallel? Answer.Line 1 has a gradient of 2 and Line 2 has a gradient of -2. Not equal gradients ∴ not parallel. |
4. If the line joining A (5, 7) and B (12, 28) is parallel to the line joining M (k, 2k) and N ( 7, 9), find the value of k. Answer.k = 14. | |
5. Which of the following lines are parallel?
Answer.Lines (i) and (iii) have gradients of 1/3. |
6. Show that the figure ABCD whose vertices are the points A (0, 2), B (6, 5), C (3, 1) and D (7, 3) is a trapezium. | |
| Parallel lines - determining equations. |
7. The line y = 3x + 2 is parallel to line L which passes through the point (5, -2).
Determine the equation of line L. Answer.y = 3x - 17. |
8. Line A has a gradient of 4 and it passes through the point (23, 42). Line B is parallel to Line A and it passes through the point (10, 11). Determine the equation of Line B. Answer.y = 4x - 29. |
| 9. A triangle has vertices at A (-3, 0), B (1, 4) and C (7, 2). Find the equation of the line parallel to the side BC which passes through the vertex at C. Answer.y = x - 5. |
10. Find the equation of the line which is parallel to the line 3x - 2y + 5 = 0 and which passes through the point of intersection of the lines 4x + y + 3 = 0 and 5x - 2y + 8 = 0. Answer.39x - 26y + 76 = 0. |
|
| 11. | 12. The line joining the points (2, 0) to (0, 4) is parallel to the tangent to the curve y = x2 + 2 at x = 1. Find the equation of the tangent to the curve. Answer.y = -2x + 5. |
|
| Perpendicular lines - testing gradients. |
13. Are the lines y = 3x + 6 and x + 3y - 7 = 0 perpendicular? Answer.Line 1 has a gradient of 3 and Line 2 has a gradient of -1/3. As product of gradients is -1, lines are perpendicular |
14. Are the lines x + y + 1 = 0 and x - y + 1 = 0 perpendicular? Answer.Line 1 has a gradient of -1 and Line 2 has a gradient of +1. As product of gradients is -1, lines are perpendicular. |
15. Which of the following lines are perpendicular to each other?
|
16. Four points are K (-2, -1), L (-4, 5), M (2, 3) and N (4, -3).
|
|
| 17. | 18. Show that the straight line ax + by + c = 0 is perpendicular to the line bx - ay + d = 0 |
|
| Perpendicular lines - determining equations. |
19. Find the equation of the line passing through the point (2, 6) and perpendicular to the line 2x - 3y + 1 = 0.
|
20. Find the equation of the lines perpendicular to x - 2y + 3 = 0 and passing through:
|
| 21. Line A has a gradient of -1 and it passes through the point (10, 11). Line B is perpendicular to Line A and it passes through the point (23, 42). Determine the equation of Line B. |
22. Three vertices of a rectangle are R (-2,2), E (6, 2) and C (-2, -3). The fourth vertex (at T) is not given. Answer.ET is y = 6 and CT is y = -2. |
|
| 23. | 24. | |
| Collinear points. | 25. Show that the points A (5, 6), B (11, 4) and C (23, -1) are collinear. |
26. Show that the points D (1, 1), E (3, -1/3) and F (-2, 3) are collinear. |
| 27. (i) Which three of the following points are collinear? L (2, 4), M (-4, -1), N (-7, -1), P (-6, -3) and Q (-2, 1). (ii) Find the value of k if (k, 5) is also collinear to those three points. Hint.Draw a reasonable sketch to obtain an idea of the three points.Answer.(i) M, P and Q are collinear. (ii) k = 5. |
28. The line AB begins with A (-1, 10) and ends at B (6, 11).
The point P (k, 2k) lies on AB. (i) Find the gradient of AB. (ii) Show that the gradient of AP is (iii) Hence find the value of k. Answer.(i) mab=1/7(ii) k = 71/13. |
|
| 29. The points A (0, 2), B (2, 1), C (-4, y) and D (x, -1) are all collinear. Find the values of x and y. Answer.x = 6 and y = 4. |
30. Show that the points W (2, 5), X (5, 6), Y (11, 8) and Z (-16, -1) are all collinear. |
|
| Concurrent lines. | 31. Are the following lines concurrent?
|
32. (i) Find the point of intersection between the lines x + 2y - 6 = 0 and 3x - 2y - 6 = 0. (ii) Find the value of k which makes the line (ii) k = ½. |
33. Are the following lines concurrent?
|
||
| 35. (i) Draw the triangle with vertices at A (-2, 0), B (4, 0) and C (2, 6).
(ii) Determine the midpoints and the gradients of the intervals AB, BC and CA. (iii) Determine the equation of the line perpendicular to each side and passing through the midpoint of each side. (iv) Are these three lines concurrent? Answer.(ii) AB has midpoint (1, 0) and gradient 0.BC has midpoint (3, 3) and gradient of -3. CA has midpoint (0, 3) and gradient of 1.5. (iii) Perp to AB: x = 1. Perp to BC: x - 3y + 6 = 0. Perp to CA: 2x + 3y - 9 = 0. (iv) All concurrent and pass through (1, 7/3). IMPORTANT.This is an inportant property in geometry - the perpendicular bisectors of the three sides of a triangle are concurrent. Hence the meeting point can be used as the centre of a circle passing through each of the vertices. Pretty cool!!. |
36. Show that the line passing through the point (2, -3) and concurrent with the lines 3x + 2y - 5 = 0 and 2x - y + 6 = 0 has a gradient of -7/3. |