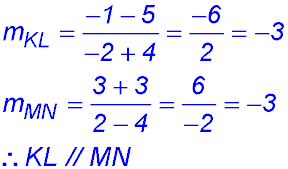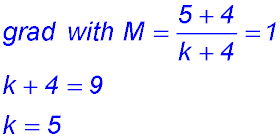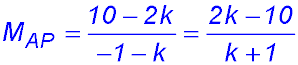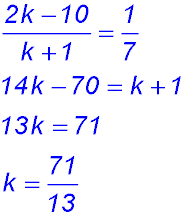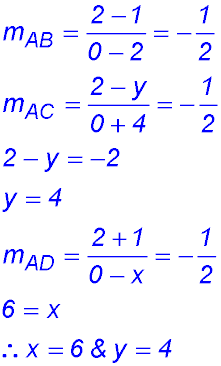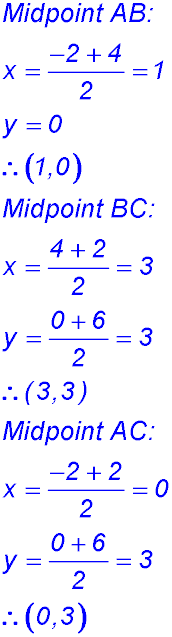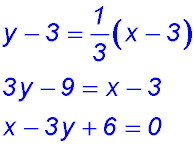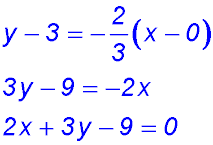Where the techniques of Maths
are explained in simple terms.
Linear functions - Testing for properties of lines.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Parallel lines - testing gradient. | 1.  |
2. 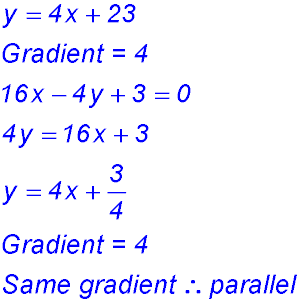 |
3. 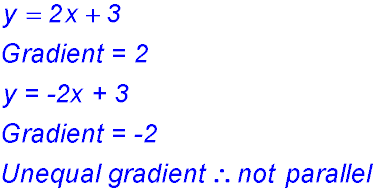 |
4. 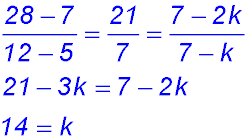 |
|
5.
|
6. 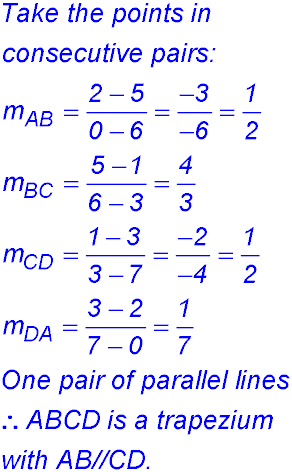 NOTE: it is good practice to calculate all four gradients because if BC // DA, the figure would have been a parallelogram which was not asked. |
|
| Parallel lines - determining equations. |
7. 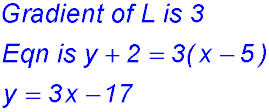 |
8. 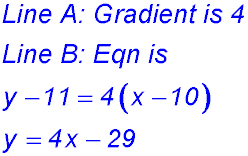
|
9. 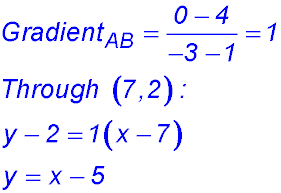 |
10. 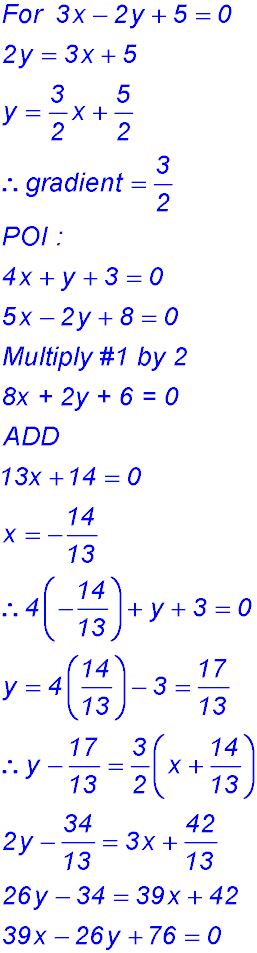 |
|
11.
|
12. The line joining the points (2, 0) to (0, 4) has gradient of -2 - the rise is 4 and run is 2 and the line slopes down. Hence the tangent to the curve has a gradient of -2. When x = 1 on the parabola Hence the equation of the tangent to the curve is: y - 3 = -2(x - 1) y = -2x + 5 |
|
| Perpendicular lines - testing gradients. |
13.  |
14.  |
15. (i) Gradient is -5.
Hence lines (i) and (iii) are parallel. Lines (ii) and (v) are parallel. |
16. (ii) (iii) (iv) (v) The quadrilateral has opposite sides parallel. So it is a parallelogram at least. KL is not perpendicular to LM so the figure is not a rectangle. The diagonals cut each other at right angles - so the parallelogram can be refined to a rhombus. See the Quadrilateral Family. |
|
| 17. | 18.  |
|
| Perpendicular lines - determining equations. |
19. 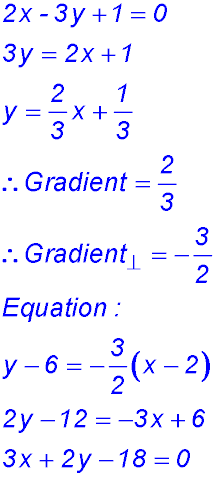 |
20. 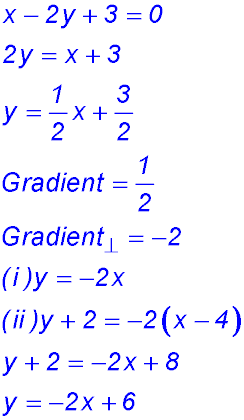 |
21. 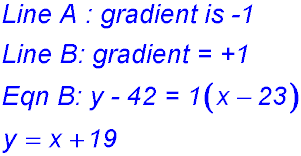 |
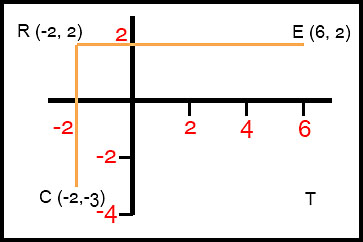
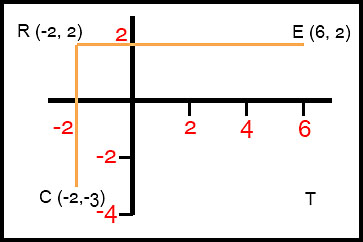
22. (ii) CT is a horizontal line parallel to RE and passing through y = -3. Hence CT is y = -3 ET is a vertical line parallel to RC and passing through x = 6. Hence ET is x = 6. |
|
| 23. | 24. | |
| Collinear points. | 25. 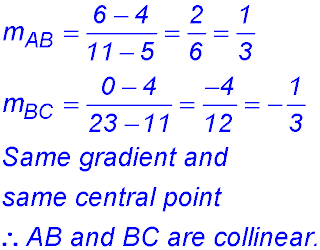 |
26. 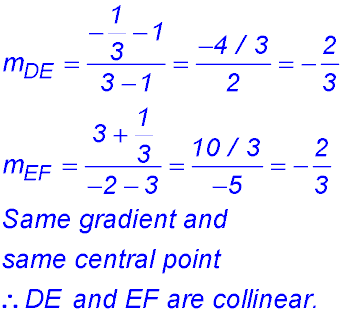 |
27. 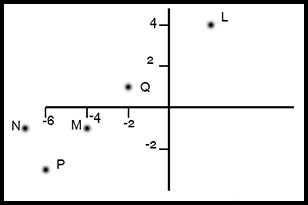
(i) The sketch gives a hint that the points could be M, P and Q. Calculate the gradients between these points:
Same gradient in each direction and point P links to both M and Q. ∴ M, P and Q are collinear. (ii) Link the new point to any of the three and calculate the gradient:
|
28. (i) 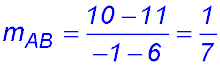
(ii) (iii) |
|
| 29. Calculate the gradient AB and then set this value against the gradients for AC and then AD:
|
30. 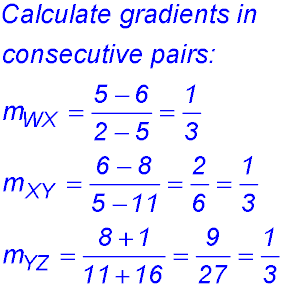
All gradients are the same and each pair is linked. Hence the four points are collinear. |
|
| Concurrent lines. | 31. Eqn (2) - Eqn (1):
Substitute into Eqn (2):
∴ all 3 lines passs through the same point. Hence they are concurrent. |
32. (i) Point of intersection between the lines x + 2y - 6 = 0 and 3x - 2y - 6 = 0.
(ii) To be concurrent, the new line must pass through the POI:
|
33. Add Eqn (1) and Eqn (2):
Sub into Eqn (1):
Sub (1, 1) into Eqn (3): LHS = 1 + 3 - 4 = 0 = RHS ∴ all 3 lines passs through the same point. Hence they are concurrent. |
34. | |
35. (i) 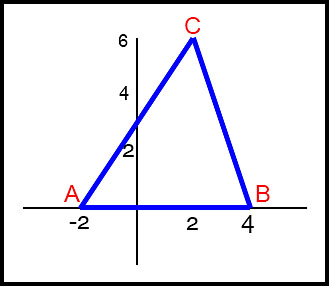
(ii) |
(iii) Determine the equation of the line perpendicular to each side and passing through the midpoint of each side. AB: Midpoint is (1, 0) and gradient is 0 (horizontal. Hence vertical bisector is x = 1. BC: Midpoint is (3, 3) and gradient is -3. Eqn of perpendicular:
AC: Midpoint is (0, 3) and gradient is 1.5. Eqn of perpendicular:
(iv) Substitute x = 1 into Eqn BC bisector: y = 7/3 Substitute x = 1 into Eqn AC bisector: y = 7/3 All lines meet at the same point so they are concurrent. |
|
36. If concurrent, the two given equations must be solved simultaneously:
|