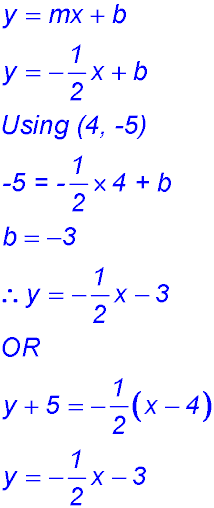Where the techniques of Maths
are explained in simple terms.
Linear functions - Determining equations.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Interpreting basic equations. | 1. y = 3x - 2. The x intercept (when y = 0) is 0.67. The y intercept (when x = 0) is -2. |
2. y = -2x + 3. The x intercept (when y = 0) is 1.5. The y intercept (when x = 0) is 3. |
|
3. 2x + 3y - 2 = 0. The x intercept (when y = 0) is 1. The y intercept (when x = 0) is 0.67. |
|
4. 4x - 5y - 1 = 0. The x intercept (when y = 0) is 0.25. The y intercept (when x = 0) is -0.2. |
|
| Given 1 point and the gradient (answer in gradient intercept form). |
5.  |
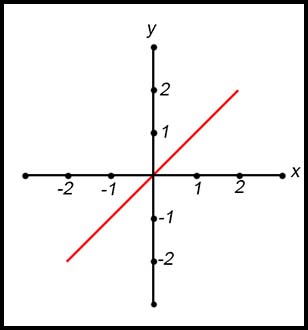
| 6.
The line shown in the graph above passes through the origin and the pints (1, 1), (2, 2), etc. Hence the gradient is 1 and there is no intercept. Hence the equation is y = x. |
|
7. 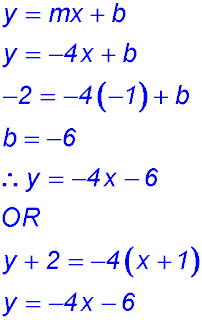 |
|
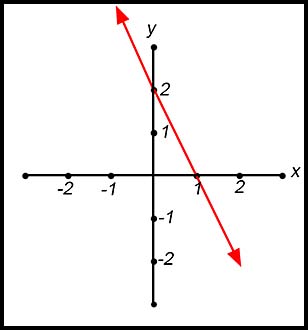
| 8.
The rise is 2 and the run is 1 and the slope is negative. Hence the gradient is -2. The y intercept is 2.
|
|
| 9. The gradient of 0 indicates the line is horizontal.
As the line passes through the point (1, -2), Hence the equation is y = -2. |
|
| Given two points (answer in general form). |
10. Determine the equation of the line shown in the graph below:
First determine the gradient between the indicated points. The rise is 3 and the run is 1 and the line slopes down. So the gradient is -3.
|
11. The line through the points (10, 3) and (15, 8) has a gradient of +1 (draw a quick sketch).
|
|
12. Quickly sketch the line through the points (-12, 3) The rise is 8 and the run is 16 and the line slopes down. Hence the gradient is -0.5.
|
|
13. Quickly sketch the line through the points (3.5, 2.7) and (5.5, 10.7). Rise is 8 and run is 2 - so gradient = 4.
|
|
14. The line through the points (3, -2) and Hence the equation is x = 3. |
|
| Given data in a table. | 15. (i) As x goes from 4 to 5 (an increase of 1), y decreases from 7 to 3 (a fall of 4). So the gradient is -4.
The equation is y - 7 = -4(x - 4). ∴ y = -4x + 23(ii) When y = -33
|
| 16. (i) For the y intercept, x = 0. Hence y = -1.
As x goes from 0 to 1, y increases from -1 to +1 (a rise of 2). So the gradient is 2. The equation is y = 2x - 1. |
|
| Given data in a diagram. | 17. From the diagram, the y intercept is 6 and the gradient is 6/3 = 2 but negative as the line slopes down. Hence the equation is y = -2x - 6 |
18. From the diagram, the y intercept is -3 and the gradient is 3/9 = 1/3 and positive as the line slopes up. Hence the equation is y = x/3 -3 or x - 3y - 9 = 0. |
|
| Given a geometrical context. | 19. The line is horizontal so all y values are the same. Hence the equation is y = 15. |
| 20. The line is vertical so all x values are the same. Hence the equation is x = 26. | |
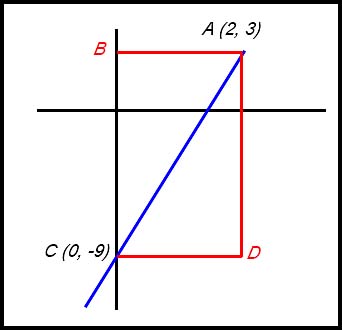
17. Draw a quick sketch. Mark in A (2, 3). The line AC is 3x - y - 9 = 0 and it cuts the y axis at -9 which is C. Now draw in the rectangle ABCD. B is horizontal from A and D is horizontal from C:
Hence B is (0, 3) and D is (2, -9). |
|
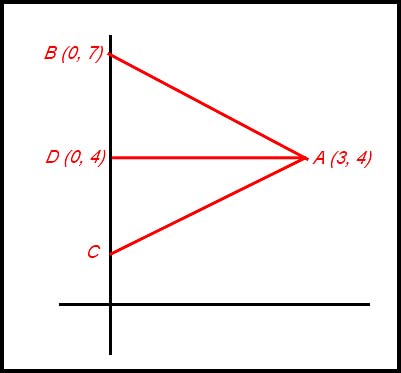
18. AD is the line from the vertex A perpendicular to the base (i.e. the y axis). It has coordinates (0, 4). Note: AD bisects the base - a basic property of an isosceles triangle. The distance DB is 3 units so DC must also be 3 units. Hence C has coordinates (0, 1). |
|
| Applications to the physical world. | 19. (i) Ish begins her saving with a deposit of $500 at time = 0. Hence that is the value to be marked on the vertical (investment) axis. Ish saves at $40 per week which is the gradient of her investment. Hence we have:
(ii) The equation to express her investment strategy mathematically is Investment = $500 + $40t (iii) Using this equation for t = 26, Ish will have saved $500 + $40(26) = $1,540 |
20. (i) The car is stationary initially - so at t = 0, speed = 0. Hence the intercept on the vertical (speed) axis is 0. The car increases its speed at a constant rate of 0.4 m/sec - and so this value is used for the gradient of the line.
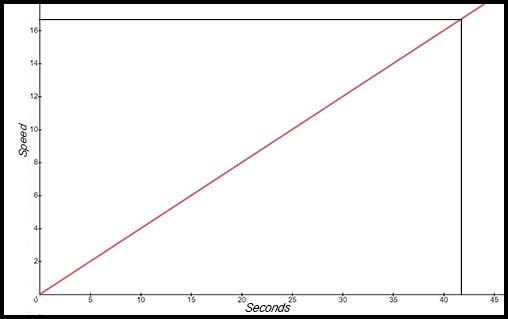
(ii) Given the above information and the basic format of the line as y = mx + b, we write the required equation linking the two variables as Speed = 0.4 × seconds (iii) Substituting into this equation: 16.7 = 0.4×Secs Hence 41.75 seconds. The graph shows the line coming from 16.7 m/sec on the vertical axis to the line and then down to nearly 42 seconds. |
|
21. (i) 6×8 + 79 = 127 cm. (ii) The gradient in a linear equation is the coefficient of the independent variable. Here that variable is AGE and the coefficient (i.e. the gradient) is 6. The value of 6 indicates that for every increase in age of 1 year (in the given age range), the height jumped by a girl is expected to increase by 6 cm. (iii) The linear equation is based (i.e. developed) on elated to girls aged from 6 to 11 years. Beyond that age range, the gradient (increase in height jumped) might not be 6 cm. The relationship would almost certainly be different. Hence a different equation would have to be developed for other age ranges - and it might not even be linear. |