Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

The equations and shapes of basic curves and functions.


 

It is VERY IMPORTANT to be able to recogise the basic form of the main functions
and associate those shapes with the relevant equation.

Use the following table to make those associations and revise them
as often as you need so you become 100% sure.

Name of function Basic form of the equation Constants Graph of the basic function.
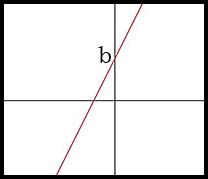
Linear y = mx + b

m = gradient

b = intercept
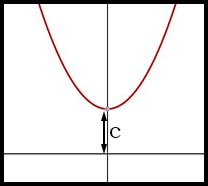
Parabola
(or Quadratic)		 y = x2 + c

c is a shifting constant.

(a, b) is the vertex.
(not required for standard or junior students) or (y - b) = (x - a)2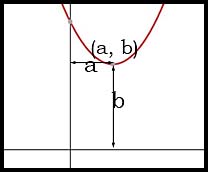
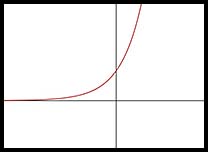
Exponential y = ax

a is any real number.

b and c are shifting constants.


Positive exponential - for growth.
  y = a -x


Negative exponential for decay/decline.
     
(not required for standard or junior students) or y = a(x - b) + c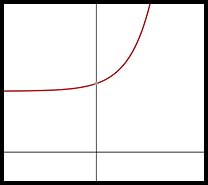
Hyperbola

or

 
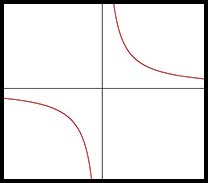(not required for standard or junior students)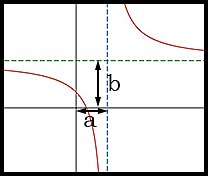  
       
Circle x2 + y2 = r2 r is the radius.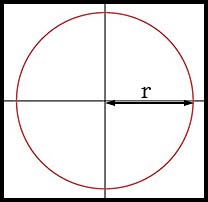
Semicircle y = √(r2 - x2)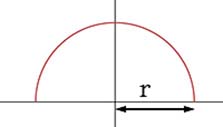

NOTE for Advanced students: The circle is not a function but its two horizontal semicircles are functions.