| The questions below require an evaluation of the continuity of a function: |
| 1. by analysing a graph. |
| 2. by analysing an equation - generally by drawing a graph of the function from the given equation. |
| Using graphs |
1.
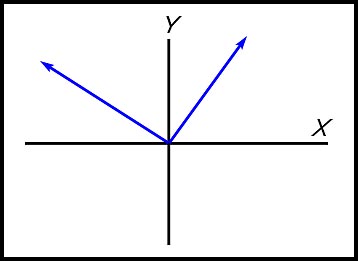
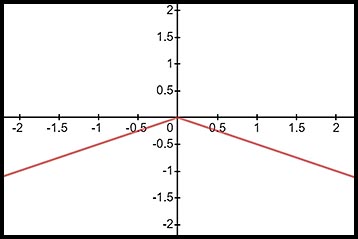
Yes the function is continuous.
The line at the left approaches 0 as x increases. The line at the right also approaches 0 as x decreases.
Hence they meet at y = 0 when
x = 0. |
2.

No the function is not continuous.
The two lines do not meet at the same point in the first quadrant. |
| |
3. The curve shown in the diagram below is continuous.
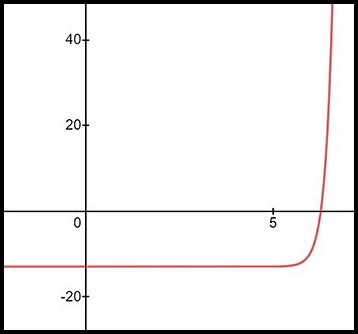
|
4. The curve shown in the diagram below is discontinuous.
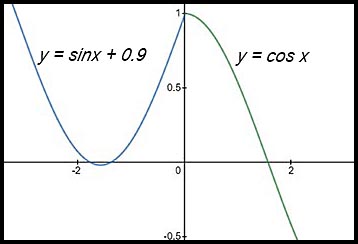
The LH sin curve cuts the y axis as y = 0.9 while the RH cos curve cuts the y axis at 1.0. |
| Using equations |
5. The linear function 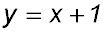 is continuous for all real x and so there is no point of discontinuity.
is continuous for all real x and so there is no point of discontinuity. |
6. The function 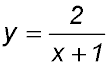 is discontinuous. Setting the denominator equal to zero is discontinuous. Setting the denominator equal to zero
gives the point of discontinuity as x = -1. The function describes a hyperbola. |
| |
7. To determine where the function is discontinuous, set the denominator = 0, factorise and solve for x:
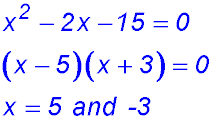
So discontinuities at x = 5 and at x = -3. |
| |
8. To determine where the curve

is discontinuous, we could set the denominator = 0. But that would not be sufficient because we can also factorise the numerator and so simplify the function:
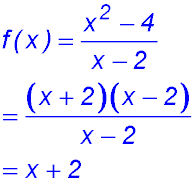
|
The function has now been reduced to a line.
Acknowledgement of the discontinuity at x = 2 needs to be included so the graph of the line would be shown as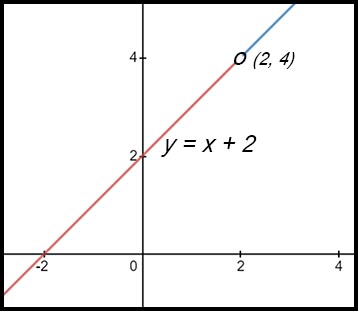 |
| |
9. The two components of the piecewise function defined by the equations
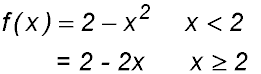
are themselves continuous.
For the first component, f(2) = -2 and for the second component f(2) = -2. Hence the function is continuous. |
10. The two components of the piecewise function defined by the equations
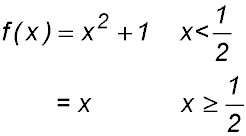
are themselves continuous.
Using the point between the two components, the first component gives 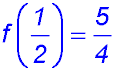 while the second is while the second is 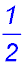 . . |
| |
11. If the function described by:
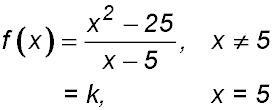
is continuous at x = 5, the values for f(5) must be equal.
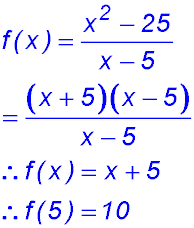
∴ k = 10 |
12. The function 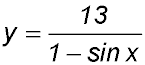 is discontinuous when the denominator = 0. is discontinuous when the denominator = 0.
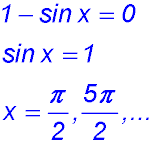
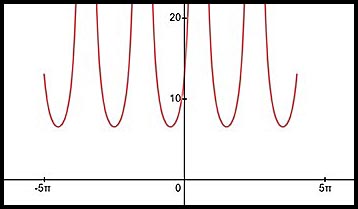
Vertical asymptotes could be drawn at the values indicated above for x - at the points of discontinuity.
|
| |
13. The function 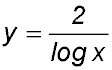 is discontinuous when the denominator = 0. So discontinuous at x = 1. is discontinuous when the denominator = 0. So discontinuous at x = 1.
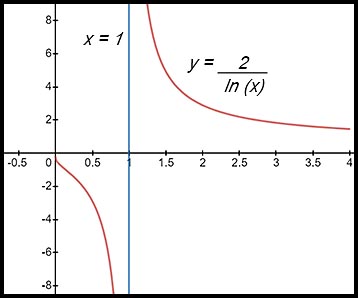
|
14. The function 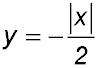 is continuous. is continuous.
|




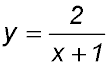 is discontinuous. Setting the denominator equal to zero
is discontinuous. Setting the denominator equal to zero
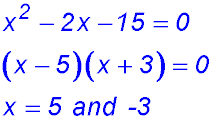

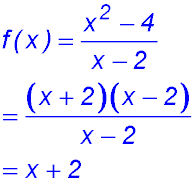

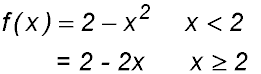
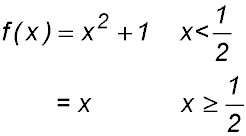
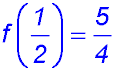 while the second is
while the second is 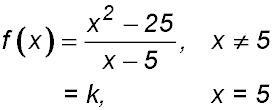
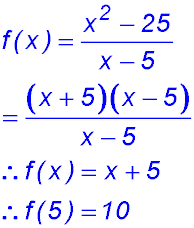
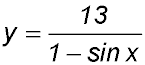 is discontinuous when the denominator = 0.
is discontinuous when the denominator = 0.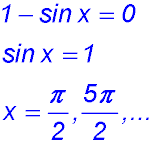

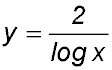 is discontinuous when the denominator = 0. So discontinuous at x = 1.
is discontinuous when the denominator = 0. So discontinuous at x = 1.
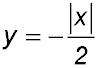 is continuous.
is continuous.