Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Functions - characteristics - even and odd functionss.
Test Yourself 1.


 

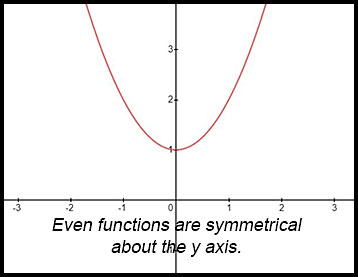
Even functions look like:

f(x) = f (-x)

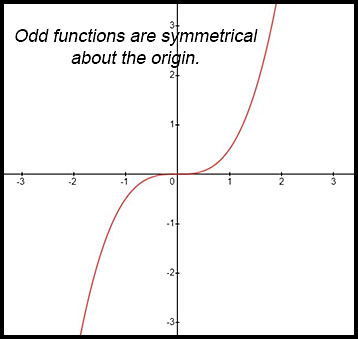
Odd functions look like:

f(x) = -f (-x)

 

Even functions 1.  
  3.  
  5.  
  7.  
Odd functions 9.  
  11.  
Graphs - given. 13.  
Graphs. 15. A function is partly defined as f(x) = 2x - 1 for x > 0.
It is also known that the function f(x) is an odd function.

(i) Complete the definition for f(x) for x ≤ 0.

(ii) Draw a neat sketch of y = f(x).

Answer.f(x) = 3x - 1 for x > 0.
f(x) = 0 for x = 0.
f(x) = 3x + 1 for x < 0.		  
 

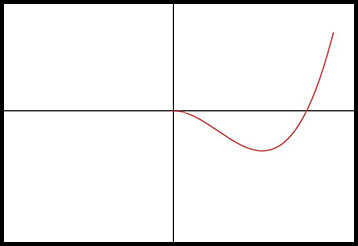
17.

The above graph shows part of the odd function y = f(x).

Sketch a complete graph of the function.

  
     
     
Even and odd functions.

23. Determine if the function

is an even, odd or neither function.

 Find a function g(x) if f(x) is an odd function and

f(x) = x2 for x > 0

f(x) = g(x) for x < 0.

Answer.g(x) = -x2.
    26. Prove 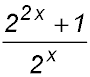is an even function.
Manipulation    
 

29. If and g(x) = x2, find the composite function f(g(x)).

State the domain and range of this composite function.