Where the techniques of Maths
are explained in simple terms.
Functions - Logarithmic - Differentiation.
Applications - Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page focus on:
|
| Gradients | 1. Show that the gradient of the curve y = loge (x2 + 1) is always positive. | |
2. Find the exact coordinates of the point on the curve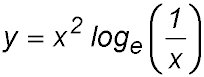 where the gradient equals zero. where the gradient equals zero.
Answer.At (1/√e, 1/(2e)). |
||
| 3. Prove that the curve y = x2 + loge 2x can never have a stationary point. | ||
| Tangents and normals | 4. Find the equation of the tangent to y = 3 loge 4x at x = 3.
Answer.y = x - 3 - 3ln 12. |
|
| 5. Find the equation of the normal to y = loge (3x - 2) at the point (1, 0) in general form. Answer.x + 3y - 1 = 0. |
||
| 6. Determine the equation of the tangent to the curve y = 2ln (2 - 5x2) at the point where x = 0. Answer.y = 2 ln 2 |
||
| 7. The function y = loge(x2) is graphed above for x > 0.
|
||
| 8. Find the equation of the tangent to the curve y = x2 ln x at the point where x = e.
Answer.y = 3ex - 2e2 |
||
| 9. | ||
| 10. | ||
| Maximum and minimum questions | 11. (i) Find the stationary point on the curve y = 4 ln (x2 + 1).
(ii) For what values of x is the concavity of this curve always positive? Answer.(i) SP at (0, 0)(ii) Positive concavity: -1 < x < 1. |
|
12. (i) Draw the graphs of y = ln(x - 1) and y = x on the same set of axes.
Answer.(ii) X = 2 (iii)D = 2. |
||
13. In the diagram,
Find the exact minimum distance for PQ between the two curves. Answer.Min PQ = 1.60 (2 dec places). |
||
14. For what value of x is the value for the ratio 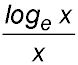 a maximum? Answer.x = e. |
||
15. |
||
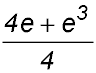 u2.
u2.