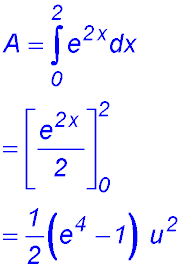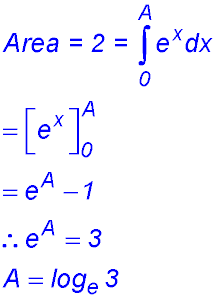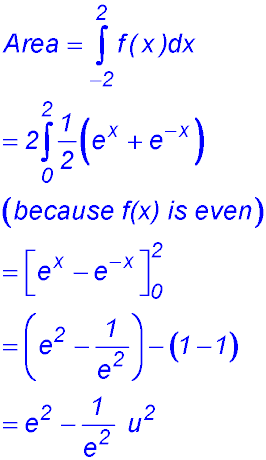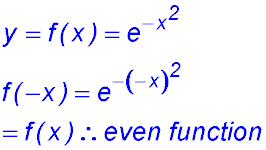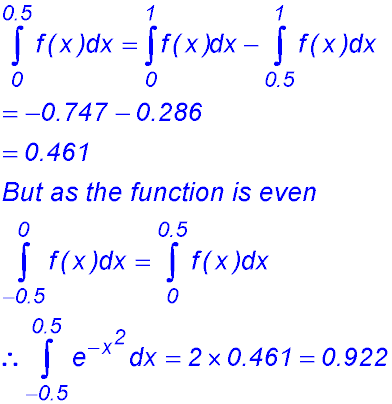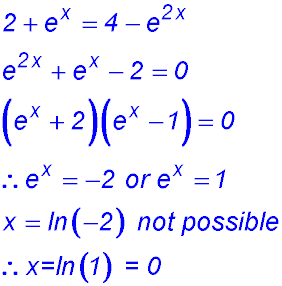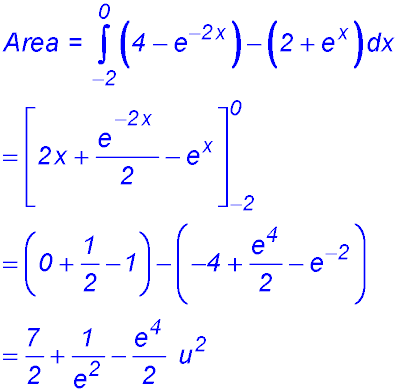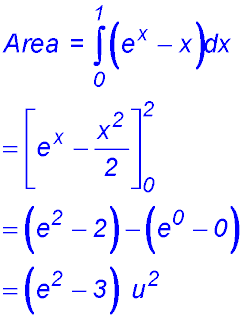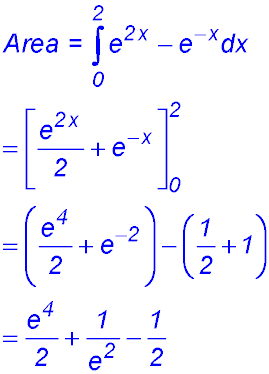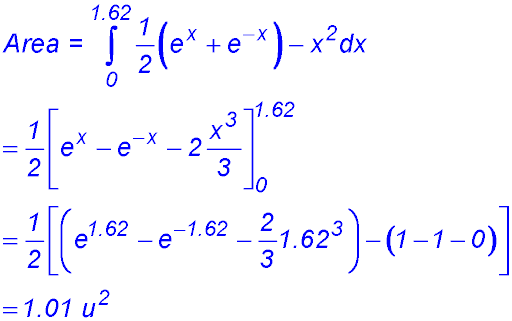Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Exponential functions - Integration - Areas.
Test Yourself 1 - Solutions.


 

The solutions on this page focus on the questions:
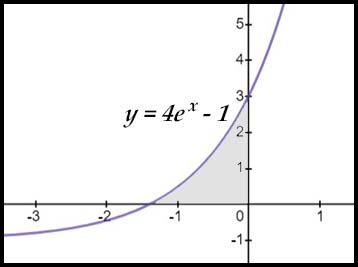
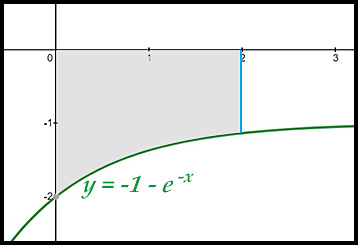
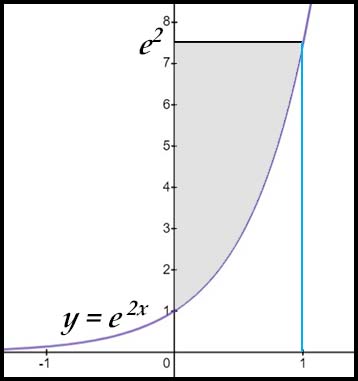
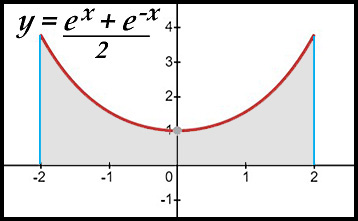
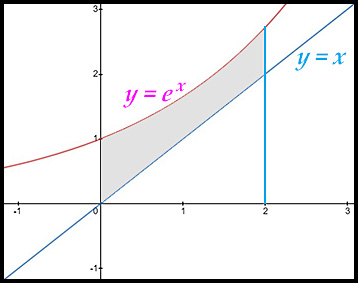
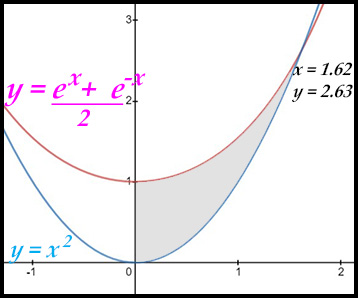
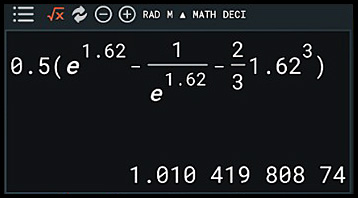
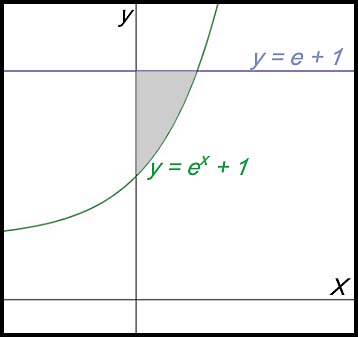
1. finding areas under one exponential curve.
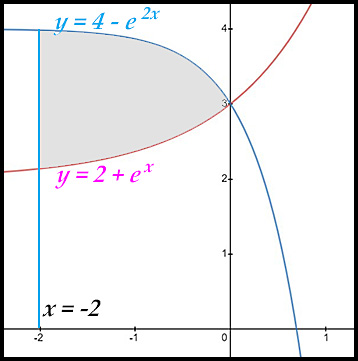
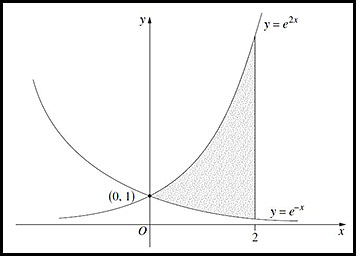
2. finding areas between two curves.
   
Areas
(1 curve)		 1.

Find the x intercept:

2.

 

Remember: Areas below the x axis are calculated to be negative so we need to take the absolute value.
  3. 4.

If we develop an equation for the required area, we will have to try to integrate a log function. Can't do that.

So we will calculate the area of the rectangle and subtract the area under the curve - which is easy to determine.
  5.

6.

 

7. (i)

(ii)

8.
  9.  
Areas
(2 curves)

10.

(i) Find the point of intersection:

(ii)

11.

 

12.

Use TOP CURVE - BOTTOM CURVE.

13.

 

14. (i)

(ii) y values are the same

∴ ex + 1 = e + 1

ex = e

∴ x = 1 and y = e + 1.

(iii)

15.