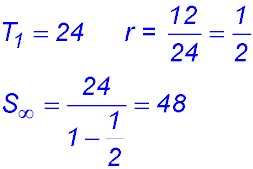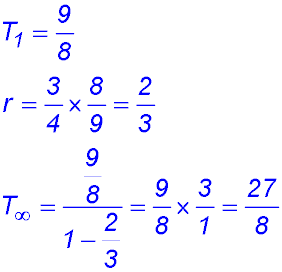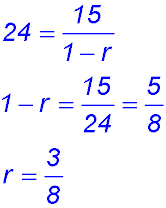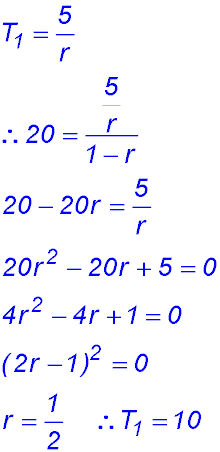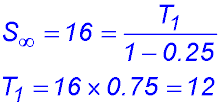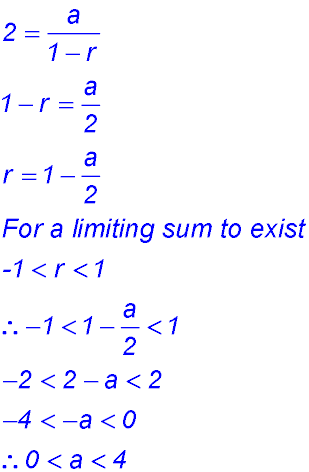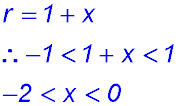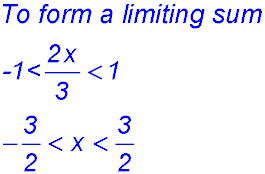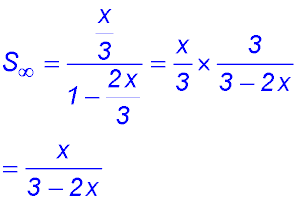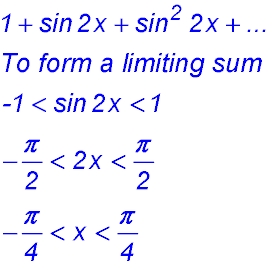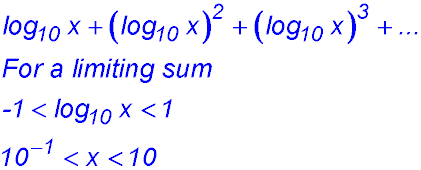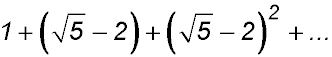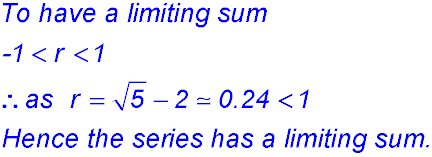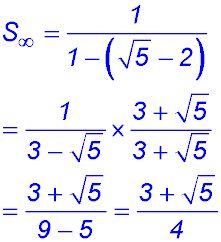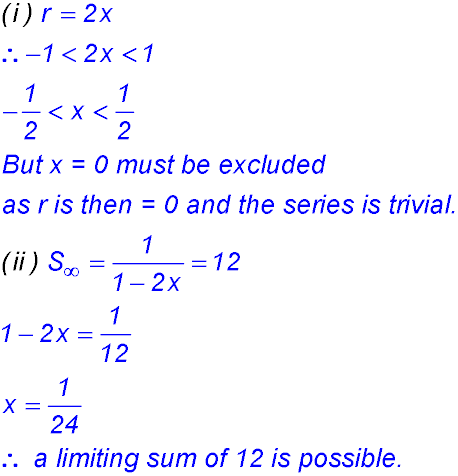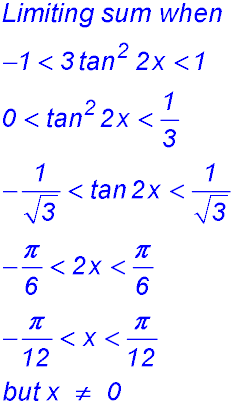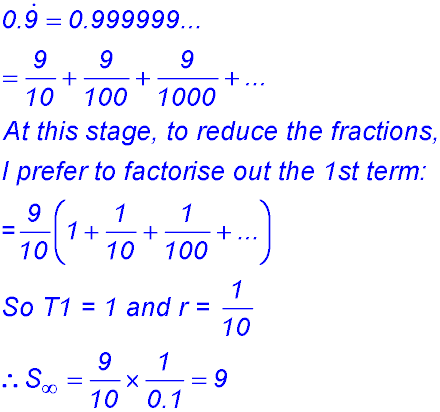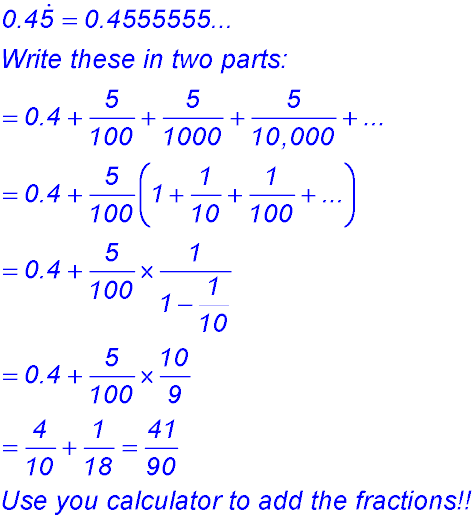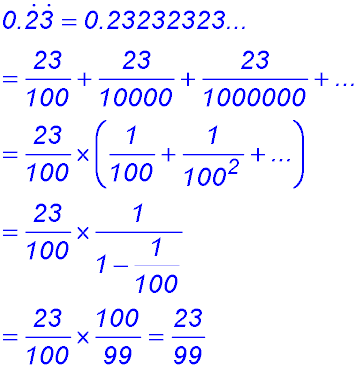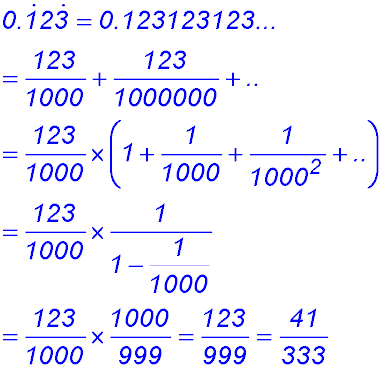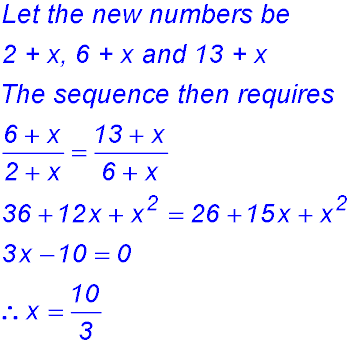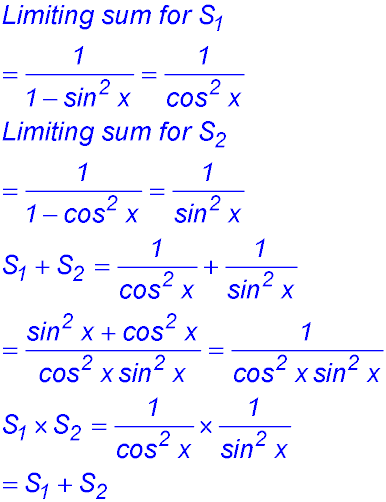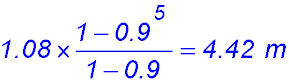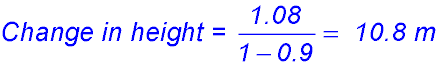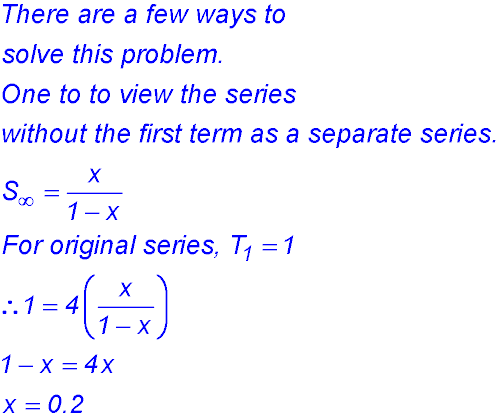Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.
Where the techniques of Maths
are explained in simple terms.
Sequences & Series - Geometric - Limiting sum.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index