Where the techniques of Maths
are explained in simple terms.
Sequences & Series - Geometric - Applied & practical questions.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| 1. An author is writing a fascinating book on
"The History of the Application of Sequences & Series to the Physical World". On the first day, she writes 54 pages. On the second day, she writes 36 pages and on subsequent days, she writes 2/3 of the number of pages written on the previous day. Answers.(i) 10.6 pages. (ii) 140.7 pages. (iii) 162 pages. (iv) See Solutions for discussion!! |
|
2. The toll on a new road tunnel is allowed, under the construction contract, to rise by 4% at the beginning of each quarter. At the beginning of the first quarter, on 1 March 2019, the toll was set at $3. The tunnel is expected to open on 4 January 2020.
Answers.(i) $3.37. (ii) $6.32. |
|
3. James is trying to fill the 1,200 litre fish tank in his backyard by carring buckets of water from the tap. He does not want to do too much work each day so:
If he continues to carry water in this way each day: Answers.(i) 9 days. (ii) No - he gets to 1000 litres. |
|
| 4. Scott is a talented high jumper. His coach wants Scott to improve his performance through meeting a series of goals.
In the first competition of the season, Scott jumps his best height to date at 1.5 m. The coach now sets Scott the goal of increasing the height of his jump by 2% at each monthly competition at which he competes from now on. Answers.(i) 1.62 m. (ii) Yes at the 16th competition. |
|
| 5. Alyssa is considering two job offers.
JOB 1: Starting salary of $30,000 and 1% pa. JOB 2: Starting salary of $20,000 and 5% pa. Answer:(i) Job 1 has a better salary after 6 years by $6,000. (ii) At the beginning of the 13th year. (iii) Job 1 by $60,000. |
|
| Limiting sum | 6. A ball is dropped from a height of 12 metres. On the first rebound, it rises to a height of 10 metres. in subsequent rebounds it rises to a height equal to 5/6 of that which it previously attained.
Answer:(ii) 132 m. |
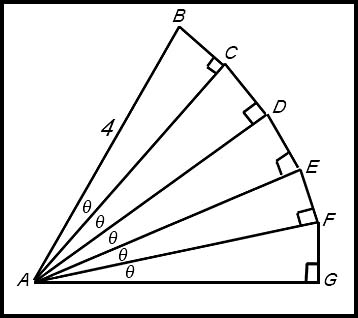
7. The triangle ABC has a right angle at C, ∠ BAC = θ and AB = 4 units.
(i) Find the length of AC; (ii) Hence show that the length of the interval AE is 4cos3 θ . (iii) Show that the limiting sum AC + AE + AG + ... is given by 4cot θ cosec θ . |
|