Where the techniques of Maths
are explained in simple terms.
Sequences & Series - Arithmetic - the General term.
Test Yourself 2.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Finding a term | 1. The first three terms of an arithmetic sequence are 7, 11 and 15.
Is 111 a member of this sequence? AnswerYes - n = 27th term. |
2. An arithmetic series begins:
84, 78, 72 (i) Is -36 a part of this series? (ii) If it is, what term number is it? (ii) -36 is T21 |
3. An arithmetic series has a sum given by Sn = 25n - 2n2.
Answer(i) T2 = 19. (iii) T132 = -501. |
||
| Finding a 1st term. | 4. | 5. |
| Finding a difference. | 6. The 6th term of an arithmetic series is 0 whilst the sum of the first 6 terms of the same series is 30.
Find the common difference and the first three terms. |
7. |
| Finding the number of terms. | 10. (i) State a formula for the sum of the interior angles of a n-sided convex polygon.
(ii) The interior angles of a convex polygon are in arithmetic progression. The smallest angle is 120° and the common difference is 5°. Find the number of sides of the polygon. Answer.No. of sides = 9 or 16. |
|
| 11. Find the number of multiples of 6 between 230 and 784.
AnswerThere are 92 multiples between 234 and 780. |
12. | |
| Given 2 terms | 13. The 8th term of an arithmetic progression is 23 and the 11th term is four times the 3rd term.
Find the first term and the common difference. Answer. T1 = 2 and d = 3. |
14.
Answer. |
| 15. | 16. | |
| Miscellaneous | 17. Given that
y2 = (2m - y)(2n - y) prove that |
18. Find the value of j such that
j + 5, 4j + 3, 8j - 2 form successive terms in an arithmetic sequence. Answer.j = 3. |
| 19. (i) Find x if
3x - 2, x, x + 10 form an arithmetic sequence. (ii) Write the first four values in the sequence. Answer.(i) x = -4(ii) Values are -14, -4, 6, 16. |
20. (i) Find the value of x if
x - 3, 5 and 2x + 1 are in arithmetic progression. (ii) Write down the three values in the given progression. (ii) Write down the two numbers which would proceed the first number and the two values which would follow the third value you have written in part (ii). Answer.(i) x = 4(ii) Values are 1, 5, 9. (iii) Preceeding: -7, -3 Following: 13, 17. |
|
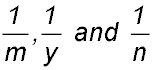 are in arithmetic progression.
are in arithmetic progression.