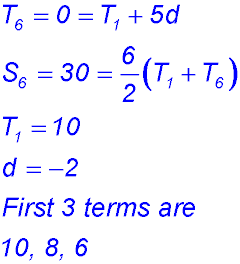Where the techniques of Maths
are explained in simple terms.
Sequences & Series - Arithmetic - the General term.
Test Yourself 2 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Finding a term | 1. The arithmetic sequence 7, 11 and 15:
So T1 = 7 and d = 4. For 111 to be a member of this sequence: 111 = 7 + (n-1)×4 108 = 4n n = 27 which is an integer. ∴ 111 is a member of the sequence. |
2. Series is 84, 78 and 72
So T1 = 84 and d = -6 ∴-36 = 84 + (n - 1)(-6) 6n = 126
So -36 is part of the series and is the 21st term. |
3. Sn = 25n - 2n2.
|
||
| Finding a 1st term | 4. | 5. |
| Finding a difference. | 6. |
7. |
| Finding the number of terms | 10. (i) Sum of interior angles = (n - 2)×180° (ii) T1 = 120° and d = 5°.
|
|
11.  |
12. | |
| Given 2 terms | 13. 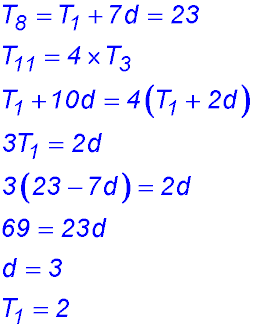 |
14. |
| 15. | ||
| Miscellaneous. | 17.  |
|
18. 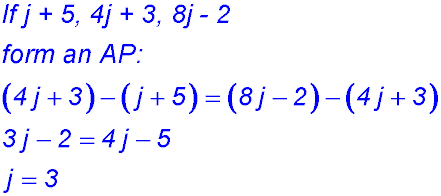 |
||
19.  |
20. 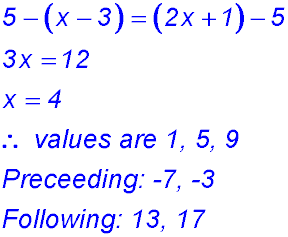 |
|