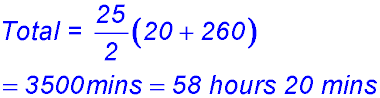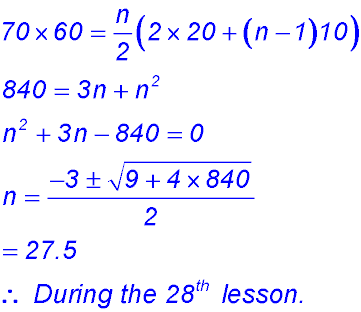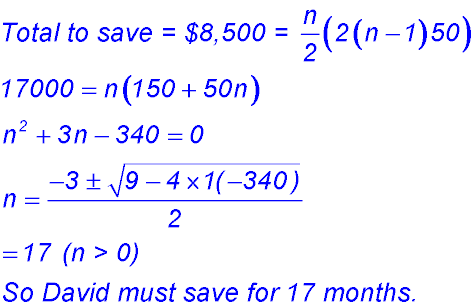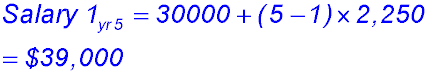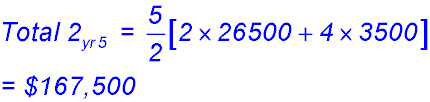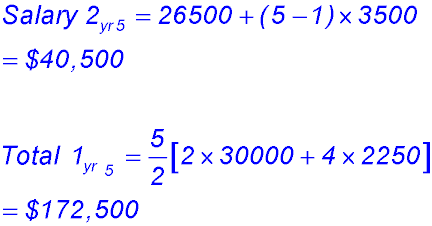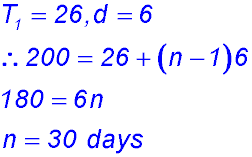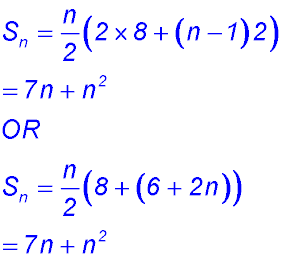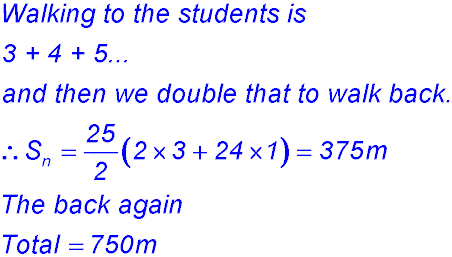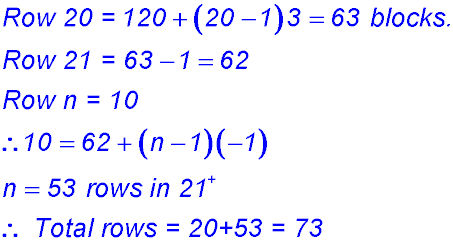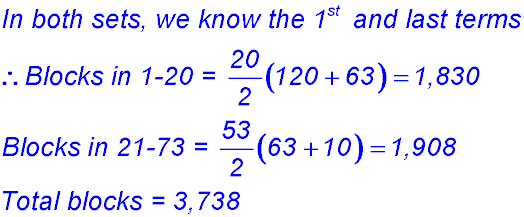Where the techniques of Maths
are explained in simple terms.
Sequences & Series - Arithmetic - Applied & practical questions.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
1. (i) 
(ii) (iii) |
2. (i) David has $7,500 and wants to reach $16,000. So he needs to save $8,500. His saving by month can be summarised as $100, $150, $200, ...So T1 = 100 and d = $50. We will calculate the sum as his savings accumulate.
100 + (17 - 1)×50 = $900. To be saving that amount of post-tax dollars might be very difficult unless David's salary had increased significantly. David might need a Plan B. |
3. (i) (ii)
(iii) To decide on the best package, Ellen needs to calculate the other two totals:
So Package 1 has a lower Year 5 salary but a higher total income. Package 2 has however closed the gap and is now higher. Hence by the end of year 7, Package 2 will be better. So its a matter of what Ellen wants. Before 7 years, she will have completed her studies and have another and better paying position. While at Uni, she needs more income. So she will probably elect Package 1 for the immediate benefits - or at least that is what she told me she would do :-) |
4. (i)
(ii) |
5. In the first year, Damien earns $600 and then $650, $700,...in an arithmetic sequence. Alyssa earns $500 in the first year and then $570, $640,...
|
6. (i) (ii) |
7. (i) (ii) |
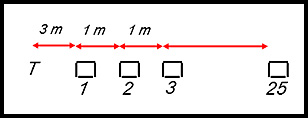
8. Draw a quick picture.
|
9. (i) No. of blocks = 180 ÷ 1.5 = 120. (ii) (iii) |
10. (i) Distance to the 3rd trough and back = 150 m × 2 = 300 m. OR T3 = 50 + (3-1)50 = 150 m × 2 = 1000 m. (ii) T10 = 50 + (10 - 1)50 = 500 m one way Total distance for the last trough = 1,000 m. (iii) |