Where the techniques of Maths
are explained in simple terms.
Calculus - Integration - Approximation methods.
Trapezoidal Rule - Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Geometric methods. | 1. Sketch the line y = 3x.
(ii) Find the area between the line y = 3x and the x-axis from x = 0 to x = 4 using a direct geometric method. Answer.Area = 24 u2. |
||||||||||||||||
| 2. (i) Sketch the line y = 5 - 2x for the domain [1, 5].
(ii) Find the area between the line y = 5 - 2x and the x axis between |
|||||||||||||||||
| 3. Find the exact area between the semi-circle Answer.Exact area = 4π. |
|||||||||||||||||
| 4. (i) Draw the parabola y = x2 + 1.
(ii) Draw a rectangle with its base on the x-axis and its top horizontal side going through the parabola at x = 0.5 and extending from x = 0 to x = 1. (iii) Draw a second rectangle with its base on the x-axis and its top horizontal side going through the parabola at x = 1.5 and extending from x = 1 to x = 2. (iv) Using each of these two rectangles, determine the approximate area between the parabola and the x axis between x = 0 and x = 2. (v) Is the area you have calculated an overestimate or an under estimate of the actual area? Explain your answer.
|
|||||||||||||||||
| 3 function values. | 5. (i) Sketch the graph of y = 2x - x2.
|
||||||||||||||||
| 6. Use the Trapezoidal rule with 3 function values to determine an approximation of the area between the curve f(x) = 2x and the x-axis between x = 0 and x = 4. Answer.Approximately 25 u2. |
|||||||||||||||||
| 7. Use the Trapezoidal rule with 3 function values to determine an approximation of the area between the curve f(x) = logex and the x-axis between x = e and x = 3e. Answer.Approximately 8.814. |
|||||||||||||||||
| 8. Find the approximate area under the function y = 1 + 2 log10 x between the values x = 1 and x = 7 using the Trapezoidal rule with 3 function values.
Answer.Approximately 12.147. |
|||||||||||||||||
9. Use the Trapezoidal Rule with three function values to find an approximation to correct to 2 significant figures. correct to 2 significant figures. Answer.Approximately 0.98. |
|||||||||||||||||
| More than 3 function values. | 10.(i) Using the x values given in the following table, complete the values for f(x) = x2 loge x to three decimal places.
(ii) Use the Trapezoidal Rule with the values in the table to obtain an approximation to |
||||||||||||||||
11. Use the Trapezoidal Rule with 5 function values as shown in the table below to find an approximation for  . .
|
|||||||||||||||||
12. A team of geologists is measuring the depth to which they must drill to take a core sample containing lithium oxide. They drill along a north-south line every 100 metres. The depths to which they drill each hole are recorded in the table below.
Answer. Area = 1.133 u2 (ii) Volume = 4.7 million cubic metres. |
|||||||||||||||||
| 13. (i) Sketch the curve y = sin 2x between x = 0 and x = 2π.
(ii) Using the trapezoidal rule, find the area between the curve |
|||||||||||||||||
14. Given the function f(x) = 3cos x, apply the Trapezoidal Rule with 4 sub-intervals to find an approximation to  . .
Answer.Approx 4.52. |
|||||||||||||||||
| Diagram | 15. The diagram shows the graph of a particle's velocity v m/sec at time t seconds. Answer.Distance = 634.9 m (approx). |
||||||||||||||||
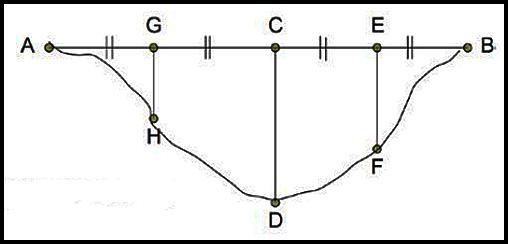
| 16. The diagram below shows a paddock ADB bounded by a river AB and three parallel fences.
The distances of each fence from the end of the paddock to the river are: GH = 8 m; CD = 12 m; EF = 10 m. All distances AG, GC, CE and EB are 5 m. Use the Trapezoidal Rule to find the approximate area of the paddock. Answer. Area = 150 m2. |
|||||||||||||||||
| 17. At a certain location along a river, the width is 20 metres. Measurements of the depth across the river at this point have been taken and these measurements are recorded on the cross-sectional diagram below.
Answer.(i) Area = 74.75 m2 (ii) 8,970 m3 in 1 hour or 8,970 ML/hpur. |
|||||||||||||||||
18. The following diagram shows the graphs of y = ln(x + 1) and  . .
Complete the following table (using your calcuator) and then calculate the area of the shaded region between the two curves from x = 1 to x = 3.
|
 .
.