Where the techniques of Maths
are explained in simple terms.
Calculus - Differentiation - Applications of Calculus.
Max/min of given equations - Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page require the determination of both the first and second derivative of given equations.
| The questions of this page focus on the following issues: |
| 1. Finding a minimum & maximum values. |
| 2. Absolute maximum/minimum values. |
| 3. Where is a curve increasing/decreasing. |
| 4. The number of solutions for an equation. |
| Minimum & maximum values. | 1. The function y = x3 - 3x2 - 9x + 1 is defined in the domain [-2, 5].
Answer.(i) Maximum at (-1, 6) and minimum at (3, -26). (ii) POI at (1, -10). |
2. The cost of running a tour ($C) for x people can be expressed as C = x3 - 972x + 20,000.
Answer.(i) Need 18 people for min cost. (ii) Min cost/person = $463.11. |
| 3. A curve is determined by the equation
y = x3 - 12x + 4. Answer.(i) Maximum at (-2, 20) and minimum at (2, -12). (ii) POI at (0, 24). (iv) Maximum value of 20 at x = -2 and at x = 4. |
4. Consider the curve y = 20 - 5x2 - x3 for [-5, 2]. Answer.(i) Maximum at (0, 20) and minimum at (-10/3, 1.48). (ii) POI at (-5/3, 10.74). (iv) Maximum value is 20 at both x = -5 and at x = 0. |
|
| Absolute max/mins. | 5. For the function f(x) = 3x2 - x3 + 9x - 2:
Answer.(ii) Maximum value at (3, 25) Minimum value at (-1, -7). (iv) Minimum value of the function is -7 and that minimum occurs at x = -1 and at x = 5 in the given domain. |
6. |
7. Consider the curve f(x) = x3 - 2x2 + x + 4 for [-2, 2].
Answer.(i) Maximum at (1/3, 112/27) and minimum at (1, 4). (ii) POI at (2/3, 110/27). (iii) (0, 4) and (-1, 0) (v) Max value is f(x) = 6. |
8. The function y = 2x3 + 3x2 - 36x + 5 is defined in the domain [-5, 5].
Answer.(i) Maximum at (-3, 86) and minimum at (2, -39). (ii) POI at (-0.5, 23.5). (iv) Maximum value is 150. |
|
9. Find both the relative and the absolute maximum and minimum values for the function f(x) = x3 - 6x2 + 9x - 5 = 0 in the domain [0, 4]. |
10. Find both the relative and the absolute maximum and minimum values for the function
f(x) = 3x4 + 4x3 -12x2 - 3 in the domain [-2, 2]. Answer.The local minimum and absolute minumum are -35 at x = -2.The local maximum is -8 when x = 0 and the absolute maximum in the domain is 29. | |
| 11. Find the absolute maximum and minimum values of the function Answer.The minimum value is 1 at x = 1 and the maximum value is 5 at x = 9. We cant do calculus with this question to obtain the values!!!. |
12. Find the absolute maximum and minimum values of the function 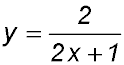 in the domain [1, 9]. in the domain [1, 9].
Answer.The minimum value is 2/3 at x = 1 and the maximum value is 2/19 at x = 9. We can't do calculus with this question to obtain the values!!!. |
|
| Curve sketching. | 13. A function is defined by 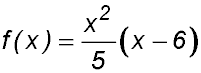 . .
Answer.(ii) Maximum at (0, 0) and minimum at (4, -6.4). (iii) curve is decreasing 0 ≤ x ≤ 4. |
14. For the curve 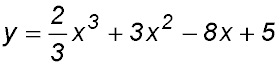 : :
|
| 15. Let f(x) = x3 + kx2 + 3x - 5 where k is a constant.
Find the values of k for which f(x) has NO stationary points. Answer.-3 < k < 3. |
16. (i) Find the derivative of
(ii) Find the value(s) of m for which the graph of
has no stationary points. Answer.-5 < m < 3. |
|
| 17. For the curve y = 7 + 5x - x2 - x3,
(i) find the co-ordinates of the maximum and minimum values. (ii) Find the point where the concavity changes. (iii) Sketch the curve. (iv) For what values of x is the curve concave down? |
18. For the curve 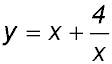 (i) Find the co-ordinates of where the maximum and minimum values occur and determine their nature. (ii) Sketch the curve. (iii) For what x values is the curve concave up. |
|
19. For the curve y = 3x4 - 8x3 + 6:
Answer.(i) Min at (2, -10) (ii) HPOI at (0, 6). and POI at (4/3, -3.48). |
20. Given f(x) = (x + 2)(x - 2)3
and f '(x) = 4(x - 2)2(x + 1) = 4x3 - 12x2 + 16 Answer.(i) Min at (-1, -27) (ii) HPOI at (2, 0) POI at (0, -16). |
|
| Number of solutions. | 21. Consider the curve y = 2x2 (x - 3)2.
Answer.(i) Max at (1.5, 10.125) Min at (0, 0) and at (3, 0). (iii) No. of solutions = 2. |
22. A function can be expressed as
f(x) = 3x4 + 4x3 - 12x2 Answer.(i) Max at (0, 0) Min at (-2, 32) and at (-1, 5). (iii) Increasing for -2 < x < 0 and for x > 1. (iv) k < -32.(v) k = 0 or k = -5. |