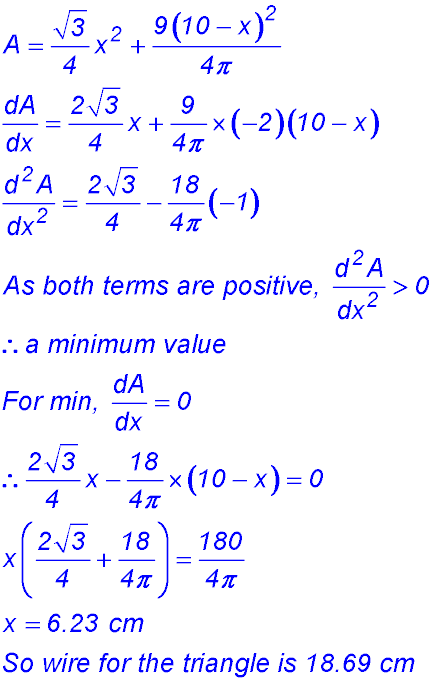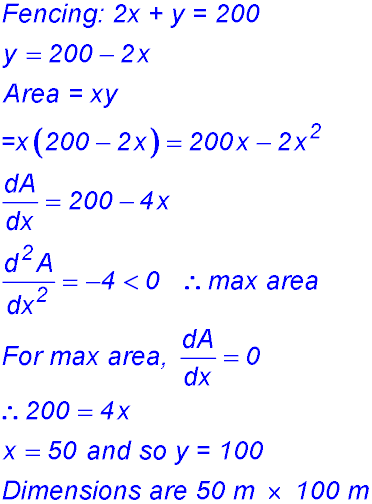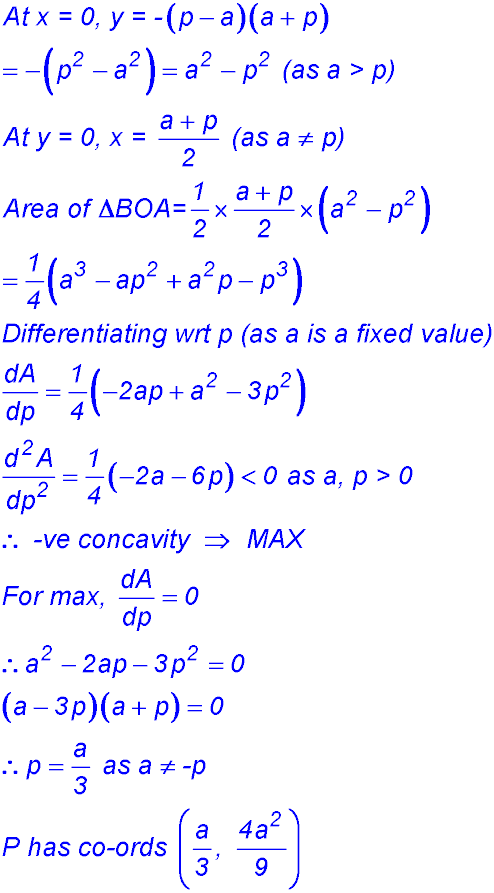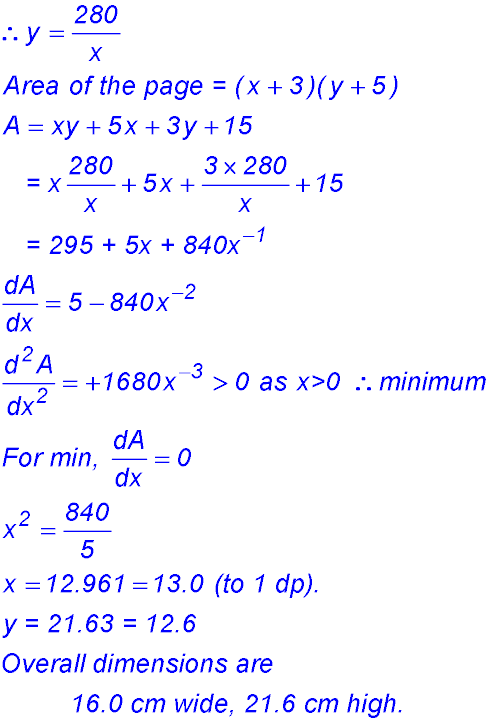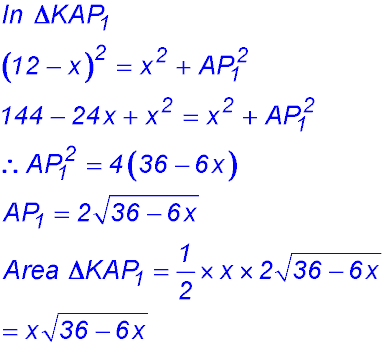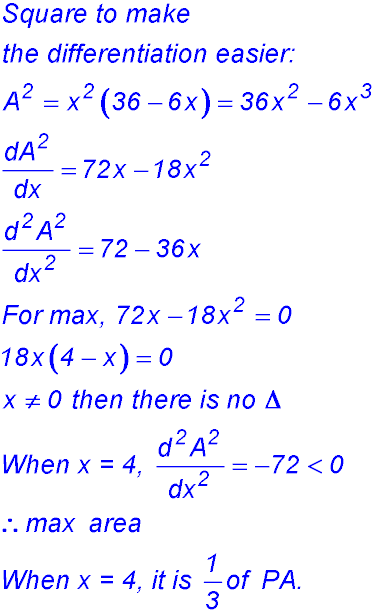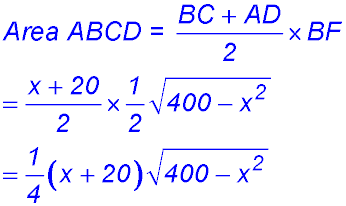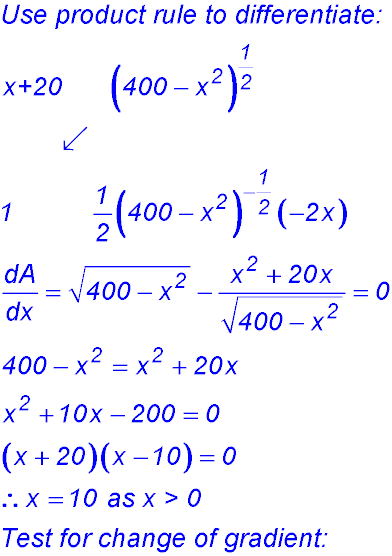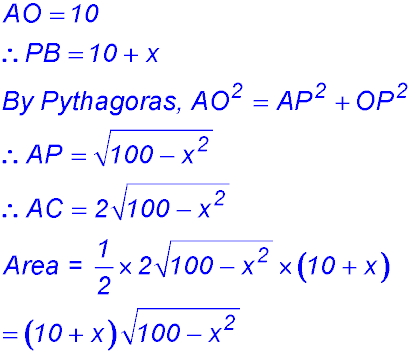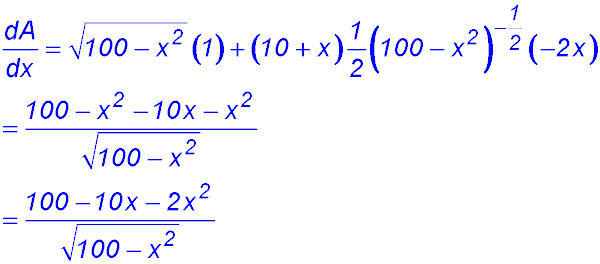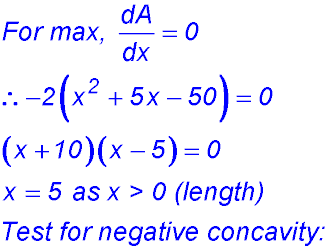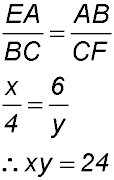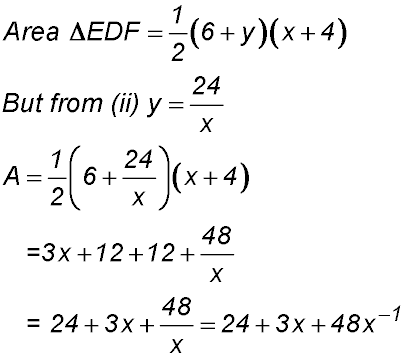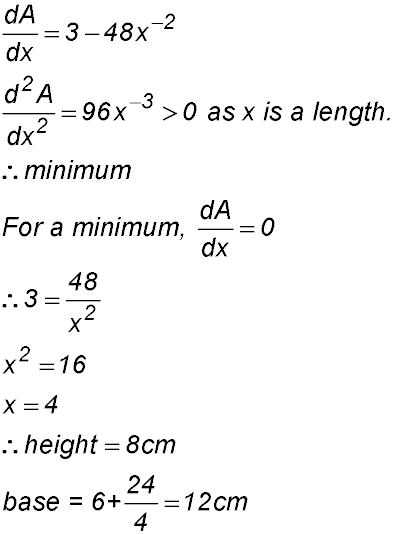Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Calculus - Differentiation - Applied max/min questions.
Type 2: 2D shapes - Test Yourself 1 - Solutions.


 

Creating 2 shapes 1. (i)

(ii)

  2.

Areas and paddocks.

3.

(i)

(ii)

 

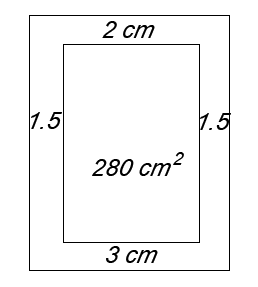
4.

Let the dimensions of the printed area be x cm wide and y cm high.

Hence area of printed material is A = xy = 280 cm2.
  5.

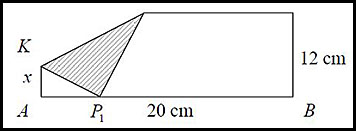
(i) PA was 12 cm long. After the fold, x cm (KA) remains vertical so the balance KP1 must be the difference - so (12 - x) cm.

(ii)

(iii)

 

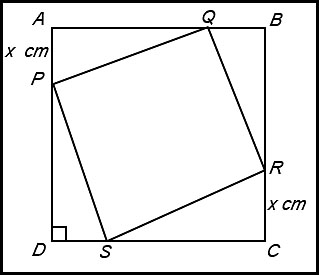
6.

(i) PD = 10 - x = AQ = BR = SC.

So we can apply Pythagoras' Theorem to calculate (say) PS.

PS2 = x2 + (10-x)2.

We could take the square root to calculate PS but,
as PS = PQ and the area of square
PQRS = PS×PQ = PS2, we do not.

So the area of the square PQRS is A = x2 + (10-x)2
Geometric shapes.

7.

 
  8. (i)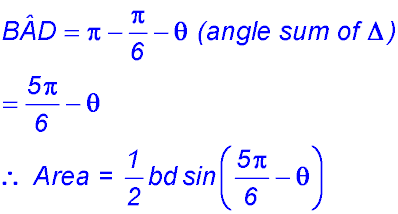

(ii)

  9. (i)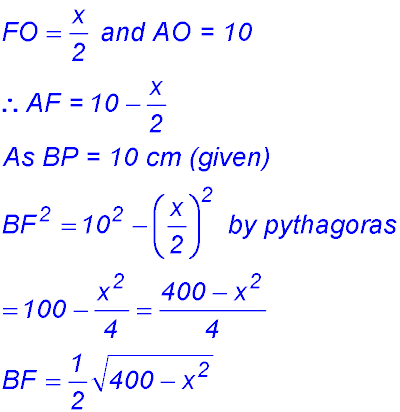

(ii)

(iii)

x 9 10 11
dA/dx -29 0 31

So change of gradient around x = 10 from -ve to +ve - hence a maximum value for A.

∴ BC = 10 cm.
 

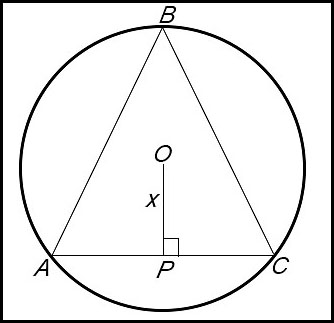
10.

(i)

(ii)

(iii)

x 4 5 6
A' 3.06 0 -4

Change of gradient -ve to +ve so a maximum value.
 

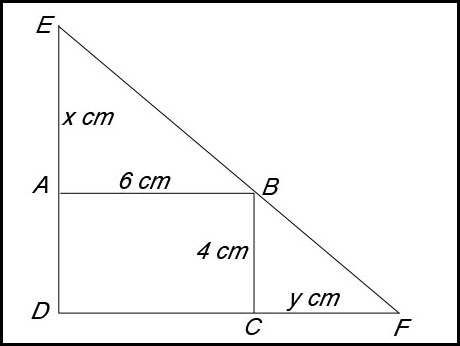
11.

(i) ABCD is a rectangle and so AB//DCF and EAD//BC.

(ii) Ratioing corresponding sides in silimar triangles:

(iii) ED = x + 4 and DF = 6 + y

(iv)
Distance between
2 curves.		 12. (i)

(ii) D = top curve - bottom curve.

= (x - 2)2 + 9 - (x(6 - x))

= x2 - 4x + 4 + 9 - 6x + x2

= 2x2 - 10x + 13

(iii)
  13.