Where the techniques of Maths
are explained in simple terms.
Applications of Calculus - basic rates of change.
Test Yourself 2.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page focus on:
|
| Given the quantity. | 1. A pool is being drained and its capacity in L litres of water at time t minutes is given by L = 120 (40 - t)2. Answer.(i) Initial mass = 200 kg. (ii)Time = 35 mins. (iii) Rate = -40/7 (or -5.71) kg/min at 11.25 secs. |
| 2. | |
| 3.
|
|
4.
Answer.(i) 23.1%. (ii)Peaks at 2 weeks. |
|
| 5. Answer.Rate = (10π)/3 cm3/sec. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| Given the rate. | 11. A chemical factory is obliged to install special filtering equipment in accordance with the Clean Air legislation.
At present the rate of emission
where t is the time in months from the date at which the new filtering system was installed. (i) What is the rate of emissions when the equipment had just been installed? (ii) What will be the ultimate rate of emissions? (iii) Calculate the total amount of emissions (to the nearest tonne) to pollute the atmosphere by the end of the first year? Answer.(i) 400 tonnes.(ii) 100 tonnes. (iii) 2,078 tonnes. |
| 12. A flat circular plate is being heated so that the rate of increase of its area - A m2 - after t hours is given by
Initially the plate has a radius of 5 metres. Express all answers in exact form. Answer.(i) Area = 25π. (ii) Area = 0.01πt2 + 25π. (iii) Radius = √(101)/2 (iv) Time = 10√5; hours. |
|
| MSC 2003 Q 8c | |
| MSC 2005 Q 8b | |
| MSC 2008 Q8b | |
| MSC 2007 Q10a | |
| MSC 2006 Q10a and MSC 2016 Q14d | |
| CSSA 1995 Q4c | |
13. A student attaches an air pressure pump to his bike tyre to inflate the tyres. The rate of change of the pressure in the tyre is given by
where t is the time after pumping has started. After 4 seconds of pumping, the pressure is 15 units.
|
|
20. The rate of fall in the price $P of shares in a particular company is given by One month after listing, the shares were selling for $24. Answer.((ii) P = $18. (iii) Rate = -$0.59 per month. (iv) Minimum price is $16. |
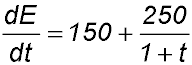
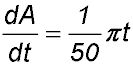
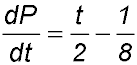 pressure units per second.
pressure units per second.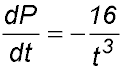 where t is the number of months after the shares were listed on the stock exchange.
where t is the number of months after the shares were listed on the stock exchange.