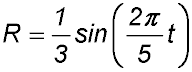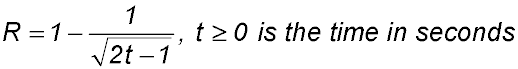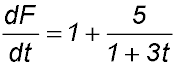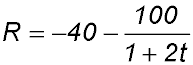Where the techniques of Maths
are explained in simple terms.
Applications of Calculus - basic rates of change.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page focus on:
|
| Given the quantity. | 1. As NBN cable is unwound from a cylinder, the mass of cable remaining on the cylinder decreases. The mass (M kg) of wire remaining on the cylinder after t minutes can be calculated by the formula Answer.(i) Initial mass = 200 kg. (ii)Time = 35 mins. (iii) Rate = -40/7 (or -5.71) kg/min at 11.25 secs. |
| 2. Some yabbies are introduced into a small dam. The number in the population can be modelled with the equation
where t is the time in months after the yabbies were introduced into the dam. (i) Show that the rate of growth of the size of the population can be described by
(ii) Find the range of the function y, justifying your answer. (iii) Show the rate of growth in the size of the population can be rewritten as (iv) Hence find the size of the population when it is growing at its fastest rate. Answer.(ii) 10 ≤ y < 200.(iv) Max rate at y = 100. |
|
| 3. An Olympic sized swimming pool is being emptied. The volume of water in the pool in litres after t hours is given by the equation
L = 312 (20 - t)3 Answer.(i) Approx. 2.5 million litres. (ii) Empty after 20 hours. (iii) Emptying at 93,600 L/hr. (iv) Maximum rate of emptying is at 20 hours. |
|
| 4. During a certain influenza epidemic, the proportion of the population in a school who are infected is given by
where t is the time in weeks since the start of the epidemic. Answer.(i) 23.1%. (ii) Peaks at 25% after 2 weeks. |
|
| 5. The volume V cm3 of a balloon is increasing such that its volume at any time t seconds is given by
Find the exact rate at which the volume is increasing at |
|
| 6. A water tank which is initially full is being emptied. The remaining quantity of water Q litres in the tank at any time t minutes after the tank starts to empty is given by
Q = 1000 (20 - t)2 where 0 ≤ t ≤ 20. Answer.(i) Q = 400,000 lit. (iii) 10 minutes. (iv) Emptying at -20,000√2 lit/min. |
|
| 7. | |
| 8. | |
| 9. | |
| Given the rate | 10. A colony of bacteria is being studied. After t seconds, the rate at which the population is changing is given by 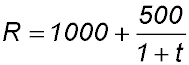 where R measures the change in the number of bacteria per second. where R measures the change in the number of bacteria per second.
Answer.(i) Rate of change when t = 0 is 1500 bac/sec. (iii) 10,200 bacteria in 1st 9 secs. |
11. A tank filled with water is accidentally punctured when an accident punctures a hole in its side. As water began to pour out, the volume of water in the tank changed at a rate of R = t2 - 9t - 10 litres/minute for 0 ≤ t ≤ T where t is the time in minutes after the accident and the water began to flow out. Initially the tank held 400 litres of water.
Answer.(i) Longest time is 10 mins. (ii) Volume = 183.33 litres. |
|
12. Oil from a cargo ship began to leak while the ship was docked in a harbour. Several hours later, authorities began the clean-up operation. The rate at which the oil was removed is described by the equation 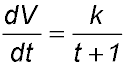
where k is a constant, t is the time in hours after the start of the clean-up operation and V is the volume of oil removed in kilolitres. By 10.00 am, x kilolitres of oil were removed. Two hours later, an additional 4 kilolitres had been removed and after three more hours, another 4 kilolitres had been removed.
Answer.(i) V = kloge (t + 1) + c. |
|
13. A spherical balloon has a radius of 20 cm. It is then inflated at a constant rate of 100 cm3 per second.
Answer.(ii) 665 secs = 11.08 mins. |
|
| 14. An adult's breathing cycle is 5 seconds long. For time t seconds, 0 ≤ t ≤ 2.5, air is taken into the lungs. For 2.5 < t ≤ 5, air is expelled from the lungs. The rate R litres/second at which air is taken in or expelled from the lungs can be modelled approximately by the equation
Using this model, how many millilitres of air does an adult take into their lungs during one breathing cycle? Answer.about 530 mls of air. |
|
15. A tank is emptied by a tap from which the water flows so that, until the flow ceases, the rate of flow after t minutes is R lites/minute where R = -(t - 6)2.
Answer.(i) 36 litres/min. (ii) 6 minutes. (iii) 1.53 mins. (iv) 72 mins. |
|
| 16. | |
| 17. A rainwater tank is initially empty. The rate R litres/sec at which water is entering the tank is given by
Answer.(ii) as R < 1, |
|
| 18. The rate at which fuel is being pumped from a full tank is given by
where F kilolitres is the amount of fuel pumped out in the first t minutes. Answer.(i) Rate = 1.2 lit/min. (iii) Amount of fuel = 13 litres. |
|
| 19. The rate R, in micrograms per minute, at which the amount of snake venom is neutralised t minutes after the injection of an anti-venom is given by
Answer.(i) Initial rate = -140 μgm/min. (ii) At 2 mins, R = -60 μgm/min. (v) Amount in 1 hour = 2,640 μgms. (vi) About 58 hours. |
|
20. A circular metal plate of area A cm2 is being heated. As it heats, the radius increases at a constant rate of 0.15 cm/h.
Answer.(i) dr/dt = 0.15. (ii) r = 0.15t + 6. (iii) A = 49π u2>. |
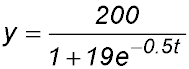
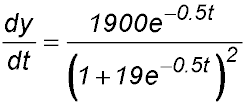
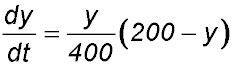 .
.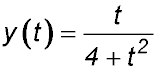
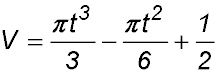
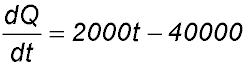 .
.