Where the techniques of Maths
are explained in simple terms.
Applications of Calculus - Equations of motion in one direction.
Test Yourself 2.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page focus on:
|
| Given a displacement equation | 1. The displacement of a particle moving along the x-axis is described by the equation
x = t4 + 4t3 - 20t2 + 1 where x is the displacement from the origin in metres and t is the time in seconds. Answers(i) At t = 0 sec, particle is at the origin with zero velocity and acceleration of 1 m/sec2. (ii) At t = 1 sec, particle is 14 metres to the left of the origin, velocity = -24 m/sec and with an acceleration of -4 m/sec2 (to the left). (iii) Particle has zero velocity but positive acceleration at t = 2. |
| 2. | |
| 3. | |
| 4. | |
| Log function | 5. A particle moves in a straight line such that its position at time t seconds is given by x = t - loget.
Answers(i) At rest at t = 1 sec. (ii) Distance = log(4/3) m. |
6. The displacement x metres of a particle moving in a straight line at time t seconds is given by x = 2t - 4 loge(2t + 1).
Answers(i) Initial velocity is -6 m/sec. |
|
| 7. | |
| Exponential eqn. | 8. The equation of motion of a particle is x = te-t where x is in centimetres and t is in seconds.
Answer.(i) t - 1. (ii) Accel = (t - 2)e-t. (iii) Acceleration = 0 when t = 2. |
| 9. The equation for the velocity of a particle moving in a straight line is The particle is initially at the origin. Answer.(iv) t = ln 5. |
|
| 10. | |
| Trig function. | 11. A particle is moving in a straight line. At time t seconds, its distancex from a fixed point P is goven by the equation:
x = 2 + 2sin(πt/4) Answer.(i) x = 2. (ii) v = π/(2√2) (iii) At t = 6, x = 2. |
12. A particle moves along a straight line so that its distance x metres from a fixed point O is given by x = t + cos t where t is the time in seconds.
Answers(i) At x = 1. | |
| 13. The motion of a particle moving in a straight line is described by the function x = 3cos 2t where x is the displacement (in metres) and t is the elapsed time (in seconds). Answer. (ii) v = -6sin 2t. (iii)v = 4.54 - so in a positive direction. (iv)Next at rest at π/2. (vi)Amplitude = 3 m. (vii) On 2 occasions. |
|
| 14. A particle moves along a straight line so that its distance x metres from a fixed point O is given by x = sin 2t - t where t is measured in seconds.
(i) What is the initial velocity of the particle? (ii) When and where does the particle first come to rest? (iii) What is the acceleration of the particle when t = π/8 seconds? (iv) What is the distance the particle has traveled when it is at rest for the second time? (iv) What is the displacement of the particle at t = 3π seconds? |
|
| Given velocity equation | 15. A particle moves in a straight line. Its velocity in metres/second after t seconds is given by  . .
Answer.(i) At t = 0, v = -2. (ii) Stationary at t = 1 so accel. = 1 m/sec2 (iv) Distance = 10 - 4ln 2. |
| 16. The velocity, in metres/second, of a particle moving in a straight line, at t seconds is given by Initially the particle is at the origin.
|
|
| 17. A particle is moving in a straight line with velocity
v = 3et - 12e-2t Initially the particle is at the origin. Time t is measured in seconds and velocity v is measured in metres/second. Answer.(i) initial velocity is -9 cm/sec. (ii) Yes at rest at (ln 4)/3 sec. (iii) Distance = 155 m. |
|
18. A particle moves in a straight line so that after t seconds (t ≥ 0) its velocity v is given by 
The displacement of the particle from the origin is v=given by x metres.
|
|
| 19. A particle is moving in a straight line. At time t seconds, its displacement is x metres from a fixed point O.
Its velocity is described by the equation v = 3t2 - 2t -1.
|
|
| 20. A particle, initially 12/π metres to the left of the origin moves along a straight line about a fixed point O so that its velocity v m/sec at time t seconds is given by
|
|
21. The velocity of a particle moving in a straight line is given by the equation v = (t - 2)2 + 5 m/sec.
|
|
| Given acceleration equation. | 22. A particle is moving with acceleration described by
It is initially at the origin and moving with a velocity of 2 m/sec Answer.(ii) 6π + 4 = 22.85 secs. |
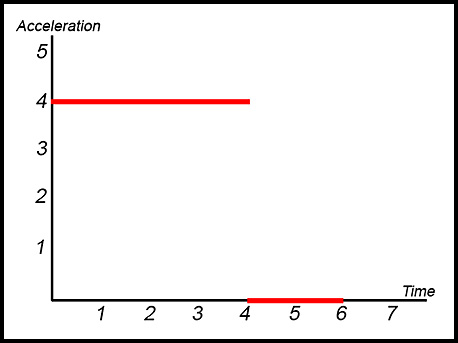
| 23. The graph below shows the acceleration of a particle during a 6 second interval.
Initially the particle is at rest at the origin. Answer.(ii) 64 m. |
|
| Two particles | |
|

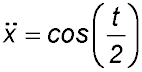 .
.