Where the techniques of Maths
are explained in simple terms.
Applications of Calculus - Natural growth and decay.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
REMEMBER: The natural growth and decay models are based on the concept that
the rate of change of a quantity varies directly with the size/amount of that quantity at any instant.
The questions on this page focus on:
|
| Growth | Direct statement | 1. The number of bacteria (P) in a colony after t minutes is given by
P = 1000 e0.04t. Find:
Answer.(i) 1490 bacteria. |
| 2. At the beginning of 2015, there were 1,200 people in the population of a small country town. A number of renewable energy companies were establishing sites in the town and it was expected that the population of the town would increase according to the model
N(t) = 1200 ekt where t is the number of years and k is a constant. At the beginning of 2019, the population had grown to 1500 people (to nearest 100). Answer.(ii) 9 years 2 months. (iii) increase in 2024 will be about 112 people per year compared to about 67 per year in 2015. |
||
| 3.The populations of two mining towns - town A and town B - have been growing during the iron ore resources boom.
Their respective populations (ii) M0 = 100 k = 1.15 × 10-4. Town A: NA = 2000 e0.13t Town B: NB = 1500 e0.18t Answer.(i) 3,800 people. (ii) In 2017. (iii) October 2019. |
||
| 4. The diameter of a tree (D cm) t years after the start of a particular growth period is given by D = 80ekt
(i) Show that (ii) If k = 0.0018, how long (to the nearest year) will it take for the diameter of the tree to measure 90 cm. |
||
| 5. In a particular native bush reserve (not too far away) the population of (unwanted) rabbits can be determined by When the first count of the rabbits was made, there were 200. After only 5 weeks, the number had increased to 440 (gestation period is about 27 days).
Answer.(i) R0 = 200; k = 0.1577. |
||
| 6. The population of butterflies in a rain forest is (thankfully) growing at an exponential rate according to the model N = 300 ekt where t is the time in months after the butterflies were first counted.
At the end of three months the number of butterflies in that area had doubled. Answers.(i) k = 0.2310. (ii) 4,800 butterflies. (iii) 140 butterflies per month. (iv) There are more butterflies than expected so perhaps the value of k has increased (which would be excellent). |
||
| Statement of derivative | 7. The rate at which Cameron's investment V is growing is proportional to the value of the investment - so 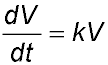 . .
(express all money answers to nearest $100).
|
|
8. The number, N, of bacteria in a culture grows at an hourly rate given by 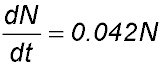 . When first placed into the dish, there were 1 million bacteria. . When first placed into the dish, there were 1 million bacteria.
Answer.(i) At 20 hours, N = 2.316 × 106. (ii) 16.5 hours. (iii) 4.2% of the number present. (iv) N = 106e 0.021t. |
||
9. The present temperature of a star is 8000° C and it is losing heat continuously. The rate of heat loss is defined by the equation 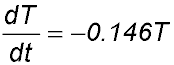 where T is the temperature in degrees Celsius and t represents time in millions of years. where T is the temperature in degrees Celsius and t represents time in millions of years.
Find the star's temperature in 10 million years. Answer. 1858°. |
||
10. The bacteria on cheese grow in direct proportion to their number B at any given time t.
Answer.(ii) k = 0.1823. (iii) 1,440 bacteria. (iv) 162 bacteria/hour. (v) 5 hours 27 minutes. |
||
| Decay | Direct statement | 11. The half-life of radium-226 is 1390 years. This means that the rate of decay is proportional to the amount present and half of any given quantity will decay in 1390 years.
The rate at which radium-226 decays is given by Answer.(i) k = -0.0005.. (ii) 3,219 years. |
| 12. The population in a country mining town was recorded at the start of 2010. The population P - t years later - is described by the exponential equation
P = 120,000 e -0.05t. (i) What was the initial population of the town at the start of 2010? (ii) Find the time, in years and months, it will take for the population to halve. (iii) At what rate is the population changing at the start of 2019?
|
||
13. The mass M grams of a radioactive isotope of carbon found in a rock sample at time t is described by the equation M = M0 e-kt where M0 and k are constants.
|
||
| 14. Ten kilograms of sugar are placed in a container of water and begin to dissolve. After t hours, the amount of undissolved sugar is given by
Answer. |
||
15. When the voltage is switched off in a television set, the current I amps flowing in the circuit decreases with time t seconds as modelled by the equation I = 0.5e-5t.
Answer.(i) 0.1433 amps (ii) 0.1386 seconds. |
||
| Statement of the derivative. | 16. A block of ice is removed from the refrigerator. The rate at which the ice melts is proportional to the amount remaining - i.e.  where M is measured in grams and time in minutes. where M is measured in grams and time in minutes.
|
|
| 17. A metal ball is fired into a tank filled with a thick viscous liquid. The rate of decrease of its velocity is proportional to its velocity cm/second.
Therefore (i) Show that v = 85 e -0.07t satisfies the equation
(ii) Calculate the velocity and the acceleration when t = 5 acc = |
||
| 18. A radioactive substance decays at a rate proportional to the amount present. After two years, 10% of the original amount has decayed.
What is the half-life of the substance (i.e. the time for 50% of the substance to have decayed)? Answer.13.15 years. | ||
| 19. After its engine is cut, a biplane travels in a straight line with negative acceleration proportional to its velocity - that is
The plane is travelling at 400 m/sec when the engine is cut and 10 seconds later the velocity is 250 m/sec.
|
||
20. A quantity Q of a radioactive substance decays at a rate that at any time t is proportional to the amount remaining at that time. That is
At t = T, the quantity of the substance has deceased to Q1.
|
.
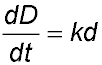 where
where 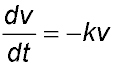 where k = 0.07 and t is the time in seconds.The initial velocity of the ball when it enters the liquid is 85 cm/second.
where k = 0.07 and t is the time in seconds.The initial velocity of the ball when it enters the liquid is 85 cm/second.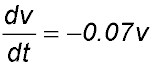
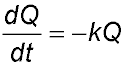 where k is a positive constant. Q0 is the amount of the substance at
where k is a positive constant. Q0 is the amount of the substance at 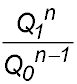 .
.