Where the techniques of Maths
are explained in simple terms.
Applications of Calculus - Natural growth and decay.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The questions on this page focus on:
|
| Growth | Direct statement | 1. P = 1000 e0.04t.
(i) the number of bacteria (to the nearest 10) when t = 10.
(ii) the rate at which the colony is increasing when t = 10.
(iii) how many minutes it takes for the colony to double in size.
Note: In questions asking doubling in size, halving in number, etc you can just use 2 or 0.5 etc rather than writing the new number and then dividing. Some questions do not give you numbers anyway - see question 11 below. |
| 2. N(t) = 1200 ekt
where t is the number of years and k is a constant.
At the beginning of 2019, the population had grown to 1,500 people. (i) Show that k = 0.0558 (correct to 4 decimal places). Note t = 4 years.
(ii) Find the time it will take for the population of the town to increase to 2,000.
(iii) At what rate was the town growing in that year compared to the rate in 2015?
|
||
| 3. The respective populations (ii) M0 = 100 k = 1.15 × 10-4. (iii) mass is about 63 grams. (iv) 26,000 years.N years after 1 January 2014 can be expressed as Town A: NA = 2000 e0.13t Town B: NB = 1500 e0.18t (i) the population of town A at the start of 2019. Note t = 5.
(ii) Find, in which year, town B's population doubled.
(iii) In which year and month did town B's population pass town A's population?
|
||
| 4. D = 80ekt
(i) Show that
(ii) If k = 0.0018, how long (to the nearest year) will it take for the diameter of the tree to measure 90 cm.
|
||
5. (i) Determine the values of R0 and k (to 4 significant figures).
(ii) Calculate the number of rabbits in the reserve after 20 weeks (to the nearest 10).
Pests!!!! (iii) How long will it take for the number of rabbits to reach 6,000?
(iv) How many rabbits per week were being added to the population after 20 weeks? Remember the rate of increase is simply Number added in week 20 = 0.1577 × 4,690 = 740 per week to the nearest whole rabbit That was enough - |
||
| 6. | ||
| Statement of derivative | 7. (i) 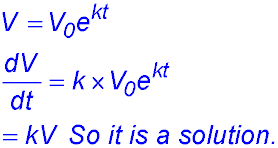
|
|
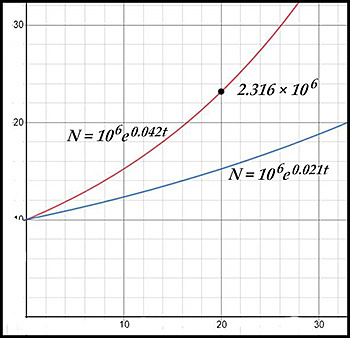
| 8. (i) Bacteria are present after 20 hours:
(iii) the percentage rate of increase of the population is 4.2% of the number in the culture at that time. (iv) The new equation for the number of bacteria is: N = 106 × e 0.021t (v) |
||
9. |
||
10. (i) The rate equation is 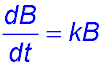 . .
(ii) To find a value for the growth constant k.
(iii) Number of bacteria on the cheese after 2 hours:
(iv) At what rate were they increasing after 2 hours? Rate of increase = 0.1823 × 1440 = 162 bacteria/hour. (v) Maximum time for the cheese to be left out (with a 10% buffer on the count): Three times is 3000 bacteria but, with the safe margin, this reduces to 3,000 × 90% = 2700.
|
||
| Decay | Direct statement | 11. (i) To find the value of k.
(ii) Number of years for 20% of the initial quantity to remain:
|
| 12. The population in a country mining town was recorded at the start of 2010. The population P - t years later - is described by the exponential equation
P = 120,000 e -0.05t. (i) What was the initial population of the town at the start of 2010? (ii) Find the time, in years and months, it will take for the population to halve. (iii) At what rate is the population changing at the start of 2019?
|
||
13. The mass M grams of a radioactive isotope of carbon found in a rock sample at time t is described by the equation M = M0 e-kt where M0 and k are constants.
|
||
| 14. Ten kilograms of sugar are placed in a container of water and begin to dissolve. After t hours, the amount of undissolved sugar is given by
|
||
15. (i) (ii) |
||
| Statement of the derivative. | 16. (i) 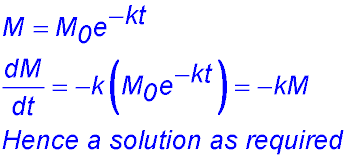
|
|
| 17.
(i)
(ii) Calculate the velocity and acceleration when t = 5:
|
||
18. 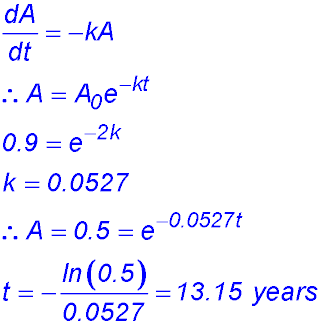 |
||
19. It the negative acceleration is proportional to its velocity - so 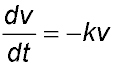 . .
|
||
20. A quantity Q of a radioactive substance decays at a rate that at any time t is proportional to the amount remaining at that time. That is
At t = T, the quantity of the substance has deceased to Q1.
|
.
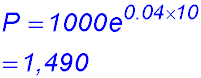

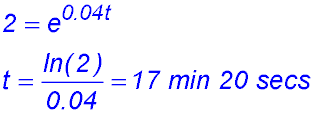
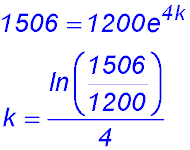
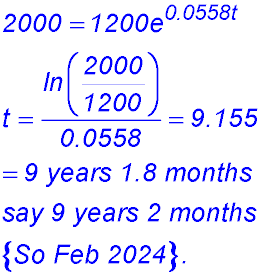
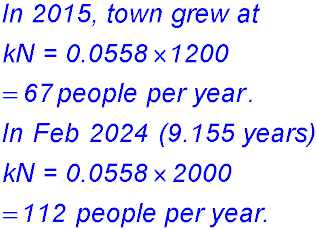
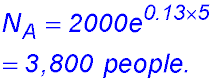
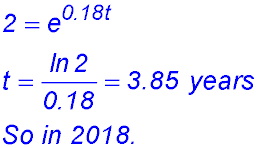

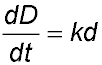 where
where 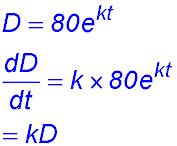
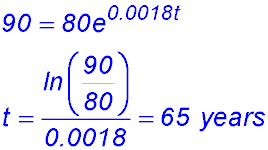
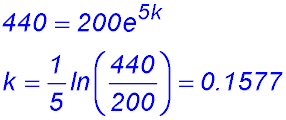
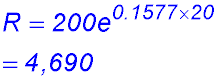
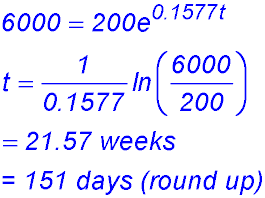
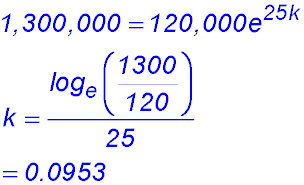

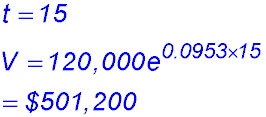
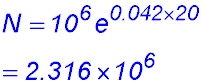
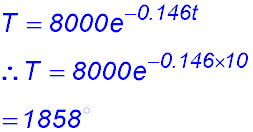
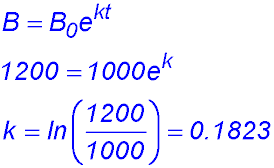
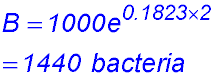

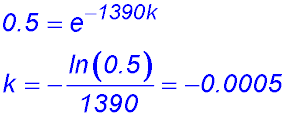
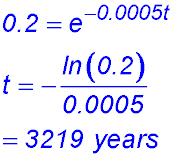
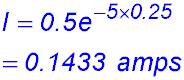
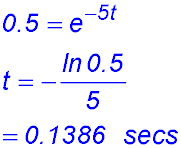
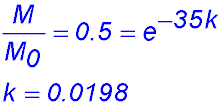
 .
.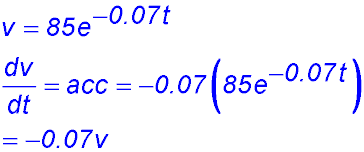

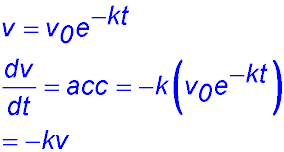 .
.
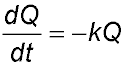 where k is a positive constant. Q0 is the amount of the substance at
where k is a positive constant. Q0 is the amount of the substance at 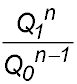 .
.