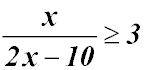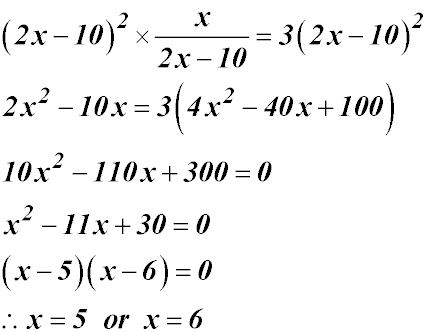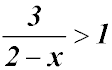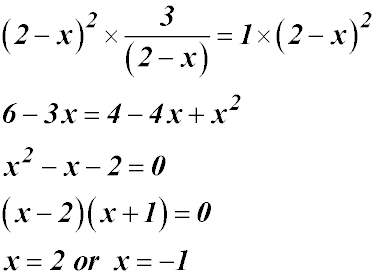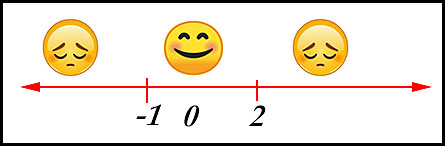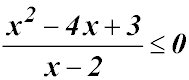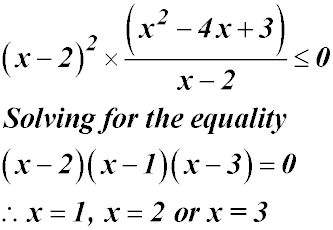Where the techniques of Maths
are explained in simple terms.
Algebra - Inequalities - Inequalities - variable in the denominator.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Multiplication can create an x2 term. |
Hence the required domain is either:
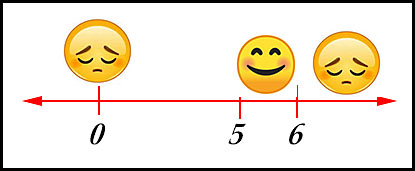
Test a number in the original inequality - 0 is easy and it is in the second domain above. We get 0 after substitution which is less than 3 - so the inequality is not satisfied (sad).
Hence the required domain is from 5 to 6. But the correct domain cannot include 5 because then the denominator would be 0 - not generally a good thing!!! So our solution is 5 < x ≤ 6. |
Hence the required domain is either:
Test a number in the original inequality - 0 is easy and it is in the first domain above. We get 1.5 after substitution which is greater than 1 - so the inequality is satisfied (so be happy).
Hence the required domain is from -1 to 2. The correct domain cannot include 2 because then the denominator would be 0 - so the fraction would be undefined!!! So our solution is -1 ≤ x < 2. |
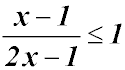 |
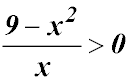 |
|
| Multiplication can create an term greater than x2. |
Hence the required domain is either:
Test a number in the original inequality - 0 is easy and it is in the second domain above. We get -1.5 after substitution into the left side which is less than 0 - so the inequality is satisfied (happy). So our solution is x ≤ 1 or -2 ≤ x ≤ 3. |
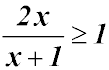 |
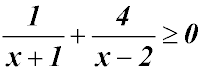 |
||
| Where on the graph of y = loge (x-2) is the gradient of the curve greater than 1. |