Where the techniques of Maths
are explained in simple terms.
Algebra - Indices and Powers.
Test yourself 3 - Advanced questions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The following questions aim to help you evaluate your understanding of the five basic concepts underlying this topic. The questions are generally more difficult and require three or more steps to complete.
Use the HINTS given if you need to.
TECHNIQUE: Be systematic in your solving of these (indeed all) mathematics problems. In questions such as those below, be systemativ and move left to right by viewing the same types of terms. For example begin with collecting the numbers and then combine the first pronumeral terms together, then the second, etc.
Take your time and write out results at each step. Its better to take a few more seconds to monitor what you are doing than to rush and do too many steps at once and therefore make mistakes.
Fractions with powers:
1. Simplify:
|
2. Simplify and express without negative indices
|
3. Simplify:
|
| 4. Solve for n:
|
5. (i) Factorise 2n+1 + 2n
(ii) Hence or otherwise write
as a power of 2. |
6.Simplify fully:
|
Powers of powers:
| 7. Expand and simplify:
(x2y + xy2)2 |
8. Expand (1 + 3n)(1 - 3n) | 9. Expand and simplify:
(m + m-1)2 |
| 10. Expand and simplify:
(2g-2f3)-2 × (2gf-3)4 |
11. Expand and simplify to prove:
(3x)-3 × (32x)4 = 243x |
12. If a = -3 and b = 5, compare the values for the expressions
a3 - 2b2 and b3 - 2a2. |
Substitution:
Do NOT just use your calculator to obtain the answer for the following questions. If you do, you will not be practicing
the essential skills.
You will get the correct answer - but so what? What is really important? No one is watching - and you know.
The other problem is that I will haunt you with my voice coming back saying "you used it - didn't you" ![]()
![]()
| 13. Evaluate the following given x = 9 and y = 25:
|
14. If x = 32 and y = 24
express 276 × 48 in terms of x and y.
|
15. If 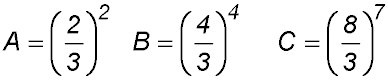
evaluate |
16. What is the value of a if
|
Solving equations:
| 17. Solve for p:
2 × 2p+2 = 16 |
18. Solve for x:
5x × 252x+1 = 125x |
19. Solve for a:
|
| 20. Solve for z:
|
21. Solve for x:
|
22. Solve for a and b:
|
Fractional indices:
| 23. Write with a fractional index:
|
24. Evaluate
|
25.
|
| 26. Rewrite using a fractional index:
|
27. Write in a format with radical signs: | 28. Write in a different format: |
| 29. (i) Expand then simplify the expression (u - v)(u2 + uv + v2).
(ii) By letting
|
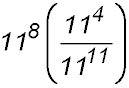
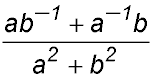
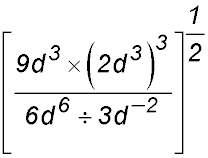
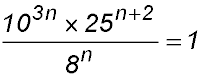
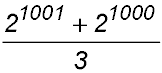
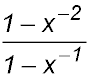
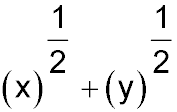
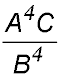 .
.
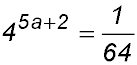
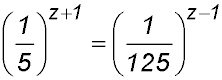
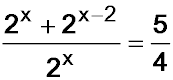
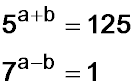
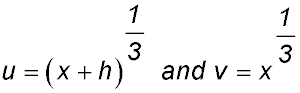 prove the following identity:
prove the following identity: