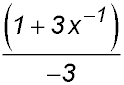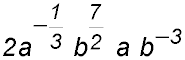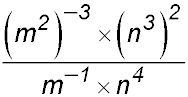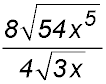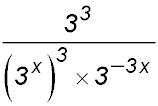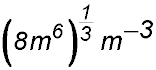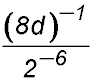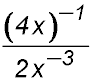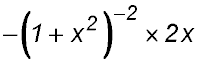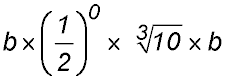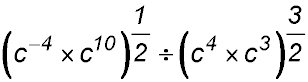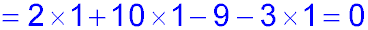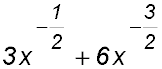Where the techniques of Maths
are explained in simple terms.
Algebra - Indices and Powers - additional basic questions.
Test yourself 2.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Simplify the following expressions to evaluate your understanding of the five basic concepts underlying this topic.
Use the HINTS given if you need to.
TECHNIQUE: Be systematic in your solving of mathematics problems. Many students just begin anywhere and then wonder why they obtain incorrect answers.
In questions such as those below, move from left to right by viewing the same types of terms. Often that requires you to collect the numbers first and then the first pronumeral terms together, then the second terms, etc. Write down intermediate results as you go. Don't try to do everything at once. Recording as you go helps you to check more easily and - in exams - you should be rewarded with showing how far you reached.
In some questions you need to express numbers in their basic factors - for example, 8 can be expressed as 23. Another common technique to use as an early step is to simplify brackets - and some comments are made here or on the Solutions page.
Fractions with Powers:
1.Simplify: 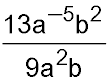 . .
Answer.13b/(9a7). |
2. Simplify: 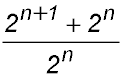 . . Answer.3. |
3. Simplify:  . . Answer.-1/x. |
4. Express in the simplest form:
 Hint.Change the values of the 24 and 6 into their basic factors and write them inside brackets. Then remove the brackets by using the indices. Answer.8. |
5. Simplify:
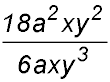 Answer.(3a)/y. |
6. Write the following fraction without using negative indices: |
7. Simplify: 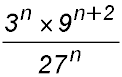 Hint.The 3, 9 and 27 should all be written as powers of 3. Then remove the brackets using the indices outside the brackets. Answer.34 = 81. |
8. Simplify 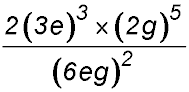 Answer.34 = 81. |
9.Simplify:
|
Powers of powers:
| 10. Simplify:
(23)5 ÷ (24)4 Hint.Start by using multiplying the indices to remove the brackets.Answer.1/2. |
11. Simplify:
(22)3 - 2 × 32 Answer.48. |
12. Simplify and express with positive exponents:
|
13. Simplify:
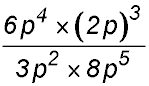 Answer.2. |
14. Simplify fully:
|
15. Simplify fully:
Answer.27. |
Negative powers:
| 16. Simplify and express without negative indices:
Answer.2/m. |
17. Simplify and express without negative indices:
|
18. Simplify and express without negative indices:
|
| 19. Simplify and express without negative indices:
Answer.x2/8. |
20. Write an expression for
without using negative indices. |
21. With respect to the following numbers,
2-(½)k, 2(½)k, 2k, 2-k and given k is a positive integer:
|
Exponents of 1 or zero:
| 22. Simplify:
2(b7)0 + 10×b0-91 - 3(x8)0 Answer.0. |
23. Evaluate:
1 - (x4+4y-3)1×(19z6)0 Answer.4 - x4 - 4y. |
24. Simplify:
|
Mixtures:
| 25. Remove the brackets from the following and simplify:
|
26. Evaluate
Answer.81. |
27. Expand
(a½ - b½)2 and answer without exponents. Answer.a - 2√(ab) + b. |
| 28. Factorise the following expression using common factors:
|
29. Find k if
k × 4x4yz3 = 20x6z8 Answer.k = 5x2z5/y.
|
30. Find the value of A if
A3 = 64m15n9p21 Answer.4m5n3p7. |