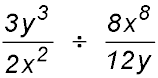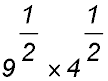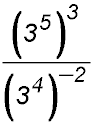Where the techniques of Maths
are explained in simple terms.
Algebra - Indices and Powers - basic questions.
Test yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Simplify the following expressions to evaluate your understanding of the five basic concepts underlying this topic.
Use the HINTS given if you need to.
TECHNIQUE: Be systematic in your solving of mathematics problems. Many students just begin anywhere and then wonder why they obtain incorrect answers.
In questions such as those below, move left to right by viewing the same types of terms. Often that requires you to collect the numbers first and then the first pronumeral terms together, then the second pronumerals, etc.
In some questions you need to simplify brackets - and comments to help you are made here or on the Solutions page.
Multiplication and division of powers:
1. Simplify: 3a × 2b × 5c × 4d
Answer.120abcd.2. Simplify: y3 × y5
Answer.y8.3. Simplify: 62 × 6-5
Answer.6-3 = 1/(63) = 1/216.4. Simplify: 2k3 × 3k4.
Answer.6k7.5. Simplify: 3x2y × 5xy3
Answer.15x3y4.6. Simplify 7 -2 × 75 × 7 -2
Answer.7.7. Simplify: .
Answer.3m/2.8.Simplify: .
Answer.(4a2)/(3b4).9. Simplify: 10x10 ÷ 5x6
Answer.2x4.10. Simplify: .
Answer.(13y3) / (x712).11. Simplify:
Answer.(9y4) / (4x10).12. Simplify: 3j2 × 2k3m2 × 3jkmn2
Hint.Start by multiplying the constant terms and record your answer. Then combine the j terms, then the k terms and so on.
Answer.18j3 k4 m3 n2.Powers of powers:
13. Simplify: (k3)5
Answer.k15.14. Simplify: (c-3)-2
Answer.c6.15. Simplify: (x-½)-2
Answer.x.16. Simplify fully: ((d2)-3)-1
Hint.Start by multiplying the inner exponents (2 × -3). Then multiply by the -1. So you move from inside to outside.
Answer.d6.17. Simplify fully: (3x2y3z)4
Hint.Expand the brackets by applying the outside exponent to each term in order.
Answer.81x8y12z4.18. Simplify fully: (2m3)3 × 4m5
Answer.324.
Negative powers:
19. Rewrite with a negative index.
Answer.-2/x.20. Rewrite -2x-1 with a positive index.
Answer.-2/x.21. Simplify: (3-1)2 × 27
Answer.3.22. Simplify .
23. Remove the brackets: (3m)-3
Answer.1/27m3.24. Simplify: .
Hint.Start by removing the negative sign from outside the brackets and simply turn the inside fraction upside down.
Exponents of 1 or zero:
25. Simplify: 50 + 1010
Answer.Sum = 2.26. Simplify: -(4m)0
Answer.-1.27. Simplify: - 7b0
Answer.-7.28. Simplify: (33)0 × 52
Answer.25.29. Simplify: 8m0 ÷ (2m)0
Hint.The first exponent of zero only applies to the m term.
Answer.8.30. Simplify: (2x3 - 4y2)1
Answer.2x3 - 4y2.
Fractional indices:
31. Write with a fractional index:
.
32. Evaluate
Answer.6.33. Write with positive indices
34. Rewrite and simplify using a fractional index:
Hint.Rewrite the square root as x to the half then add the exponents.
35. Write in a format with radical signs: .
36. Write in a different format:
.
Mixtures:
37. Simplify: (3t)2 × 4t3
Answer.36t5.38. Simplify: .
Answer.49.39. Simplify:
Answer.323.40. Simplify: 15m4n5 ÷ 5m2n4
Answer.3m2n.41. Simplify: (3g3)3 ÷ (g2)4
Hint.With this question and the next, expand the brackets first by multiplying the exponents then change to negative indices for the divisions. Remember to keep working left to right in a methodological way and do not try to do too much at once.
Answer.27g.42. Simplify: (10x2y-2)3 ÷ (2x-1y3)2
Answer.250x8.