Where the techniques of Maths
are explained in simple terms.
Algebra - Indices and Powers - basic questions.
Test yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
On this page, we have solutions to the expressions in the test aimed to evaluate your understanding of the five basic concepts underlying this topic.
Many of the solutions are presented showing the actual operations on the exponents. Very often we can just do these in our head - as long as they are easy to YOU - and avoid losing time. Instead of writing 1 + 3 but writing 4 instead, you save time. Any teacher will accept the 4 as being correct. If you do not write a 4, your teacher knows where you have made an error (e.g. a 3 indicates you multiplied). It is always a balance of time versus being careful. Do not overdo one of these actions at the expense of the other.
Multiplication of Powers:
Remember, by the First Law, we add the exponents attached to the same base.
| 1. 3a × 2b × 5c × 4d = 120 abcd | 2. y3 × y5 = y(3+5) = y8 | 3. 62 × 6-5 = 6(2-5) = 6-3 |
| 4. 2k3 × 3k4 = 6k(3+4) = 6k7 | 5. 3x2y × 5xy3
= 15 x(2+1) y(1+3)=15x3y4 |
6. 7-2 × 75 × 7-2
= 7(-2+5-2) = 71 = 7 |
7. 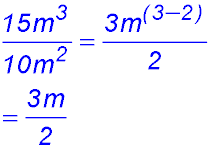 . .
|
8. 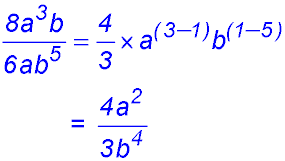 . . |
9. 10x10 ÷ 5x6
= 2x(10-6) = 2x4 |
10. 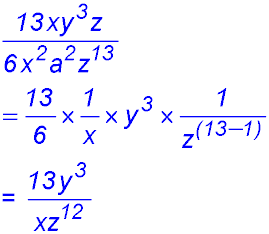
|
11. 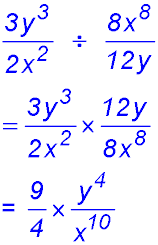 . . |
12. 3j2 × 2k3m2 × 3jkmn2
= 18j(2+1) k(3+1) m(2+1) n2 = 18j3k4m3n2 |
Powers of powers:
| 13. (k3)5
= k3×5 = k15 |
14. (c-3)-2
= c(-3×-2) = c6 |
15. (x-½)-2
= x(-½)(-2) = x1 = x |
| 16. ((d2)-3)-1
= (d(2×-3))-1 = d(-6×-1) = d6 |
17. (3x2y3z)4
= 34x(2×4)y(3×4)z4 |
18. (2m3)3 × 4m5
= 23m(3×3)×4m5 |
Negative powers:
19.  |
20. 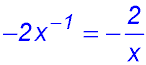 . . |
21. (3-1)2 × 27
= 3-2 × 33 = 31 = 3 |
22. 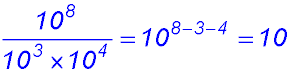 |
23.
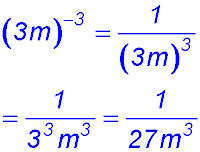 |
24. 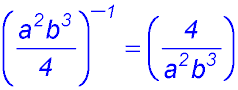
|
Exponents of 1 or zero:
| 25. 50 + 101 = 1 + 10 = 11 | 26. -(4m)0 = -1 | 27. 4a0 - 7b0 = 4 - 7 = -3 |
| 28. (33)0 × 52 = 1 × 25 = 25 | 29. 8m0 ÷ (2m)0 = 8 ÷ 1 = 8 | 30. (2x3 - 4y2)1 = 2x3 - 4y2 |
Fractional indices:
31. 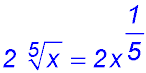 . . |
32.  |
33.  |
34. 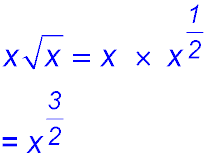 |
35. 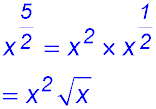 . . |
36. 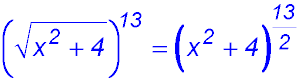 |
Mixtures:
| 37. (3t)2 × 4t3 = 9 t2 × 4 t3
= 36 t5 |
38. 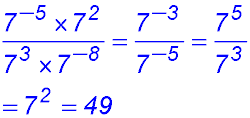 |
39.  |
| 40. 15m4n5 ÷ 5m2n4
= 3 m(4-2) n(5-4) = 3 m2 n |
41. (3g3)3 ÷ (g2)4
=33g9 ÷ g8 = 27g |
42. (10x2y-2)3 ÷ (2x-1y3)2
= (103 x6 y-6) ÷ (22 x-2y6) = 250 x(6+2) y(-6-6) = 250 x8 y-12 |