Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Algebra - Factorisation - Completing the Square.
Steps to follow.


 

1. Basic monic expression or equation.

Task: Complete the square on x2 - 6x + 5.
Step 1: Open a bracket and write an x. (x
Step 2: Copy the sign before the x-term. (x -
Step 3: Halve the number in front of the x (6 ÷ 2) = 3. (x - 3
Step 4: Complete the brackets and square. (x - 3)2
Step 5: Take off the number you just created - here 32 so subtract 9.

It is ALWAYS subtract!!

 (x - 3)2 - 9
Step 6: Copy anything following the first 2 terms in the original - here +5. (x - 3)2 - 9 + 5
Step 7: Tidy up. (x - 3)2 - 4
     
If you have an expression to factorise, you have completed your task.
     
If you are solving the equation x2 - 6x + 5 = 0:
  Copy your factorisation and put it = 0. (x - 3)2 - 4 = 0
  Solve in the normal way: (x - 3)2 = 4

x - 3 = + 2 or - 2

∴ x = 5 or x = 1

REMEMBER: look again at the videos if you are not sure of any of these steps.

 

2. Non-monic expression or equation.

Task: Complete the square on 2x2 - 7x + 3.
Preliminary step: Factorise out the coefficient of x2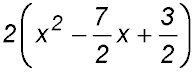
Step 1: Inside the main brackets, open another bracket and write an x.
Step 2: Copy the sign before the x-term.
Step 3: Halve the number in front of the x (7/2 ÷ 2) = 7/4.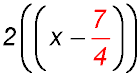
Step 4: Complete the brackets and square.
Step 5:

Take off the number you just created -

here (7/4)2 so subtract (49/16).

Its ALWAYS subtract!!
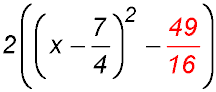Step 6: Copy anything following the first 2 terms in the original - here +5.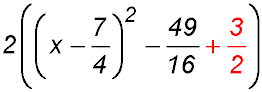
Step 7: Tidy up.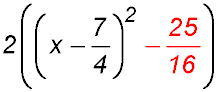
     
If you have an expression to factorise, you have completed your task.
     
If you are solving the equation 2x2 - 7x + 3 = 0:
  Copy your factorisation and put it = 0

and then solve in the normal way:
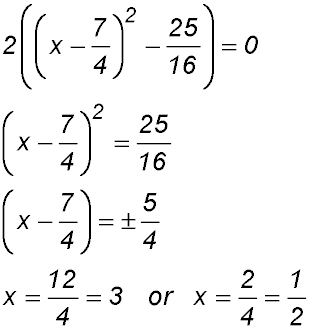